Arbre

Introduction

Une famille de lapin, dont le père s'appelle Bob et la mère Alice, ont des enfants, qui a leurs tours auront des enfants, qui se marieront et auront aussi des enfants. Comment organiser cette famille afin de visualiser qui est marié avec qui, qui sont les parents, qui sont les enfants, combien un couple a-t-il d'enfants, etc. ? Vous connaissez sans doute déjà la réponse, dans notre cas on utilisera un arbre généalogique, vous en avez forcément déjà vu et/ou construit, et cette structure devrait vous être familière.

Mais je vais vous présenter une structure de données plus large que l'arbre généalogique, qui permet de répondre à de nombreux autres problèmes et qui possède beaucoup de variantes : l'arbre.

Principe d'un arbre

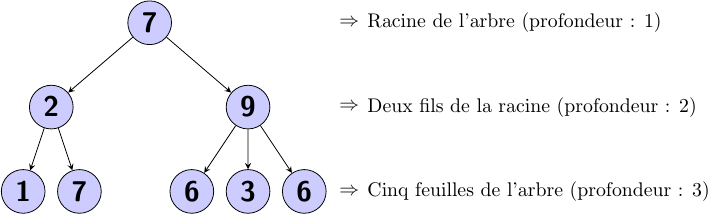
Un arbre (tree en anglais) est une structure de données permettant de représenter une hiérarchie. Chaque élément d'un arbre est appelé un nœud, et ils peuvent être reliés par des arêtes à plusieurs nœuds enfants qu'on appelle fils (le nœud parent est appelé père, et le premier nœud de l'arbre est la racine, c'est le seul élément ne possédant pas de père). Si le nœud ne possède aucun fils, on parle alors de feuille.

La profondeur d'un nœud est le nombre de nœuds le séparant de la racine, et la hauteur d'un arbre est simplement la profondeur maximale de ses nœuds.

Finalement, un arbre peut être vu comme un graphe particulier (c'est-à-dire orienté, acyclique et avec comme contrainte que chaque nœud ne possède pas plus d'un père).

Implémentation

Comme nous avons vu qu'un arbre est un graphe particulier, on peut donc l'implémenter de la même façon, je vous invite donc à lire la partie Implémentation de mon article sur les graphes pour voir et comprendre les différentes possibilités (matrice d'adjacence, liste d'adjacence et liste d'arcs).

Parcourir un arbre

De même, parcourir un arbre revient à parcourir un graphe, on peut donc utiliser les deux algorithmes de parcours de graphe :

• Parcours en profondeur : DFS (Depth First Search)
• Parcours en largeur : BFS (Breadth First Search)

Variantes

Un arbre possède énormément de variantes, qui elles même possèdent des sous variantes, c'est ce qui rend cette structure de données si importante à connaître et à maitriser :

• Arbre binaire : aucun nœud ne peut avoir plus de deux fils (d'où son nom d'arbre binaire), ceci est la base de beaucoup d'autres variantes possédant des applications en termes de recherche, de tri, de stockage, etc.
• Tas : un arbre organisé selon différentes règles afin d'être soit maximal, soit minimal, utile pour chercher le plus grand/plus petit élément dans un tableau rapidement.
• Arbre de recherche : un arbre facilitant la recherche d'éléments, ce dernier possède plusieurs sous variantes plus ou moins optimisées en fonction des différents besoins et des données.
• Trie : un arbre dit préfixe, qui stocke des chaînes de caractères (ou de simple caractère) dans ses nœuds, ce qui est pratique pour implémenter un dictionnaire de mots, ou pour faire un tri lexicographique.

Conclusion

L'arbre est donc une structure de données élémentaire (que l'on peut considérer comme un graphe avec des propriétés spécifiques), s'appliquant dans plusieurs domaines et permettant d'implémenter une hiérarchie :

• Votre système de fichier doit sans doute utiliser un arbre pour représenter les dossiers, les sous dossiers et les fichiers de votre disque dur. Sous Linux par exemple, la racine de votre ordinateur est /, et vous pouvez accéder à vos fichiers en indiquant la liste de dossiers à suivre en partant de la racine /home/utilisateur/Documents/.../fichier.
• Pour rechercher des éléments, un arbre peut être une structure très intéressante, permettant une recherche en \(O(\log _2 N)\), il est d'ailleurs la base d'algorithmes de tris (comme le tri par tas).
• Quand vous tapez une phrase et que votre moteur de recherche la complète, il utilise sans doute un arbre (et plus particulièrement un trie), afin de stocker efficacement les différentes possibilités de recherche en fonction de différents critères (nombre de fois recherché, nombre de liens en rapport, etc.).
• Parser une expression peut être compliqué, et un arbre semble parfaitement adapté pour pratiquer une analyse syntaxique sur des expressions (en mathématiques par exemple, pour interpréter une expression non parenthésée et en gérant les cas de priorités d'opérations).
• Dans un routeur, une table de routage sera utilisée afin de joindre un autre réseau, et cette dernière utilise un arbre pour stocker les informations sans trop utiliser de mémoire (à la manière du dictionnaire, c'est-à-dire grâce à des préfixes).