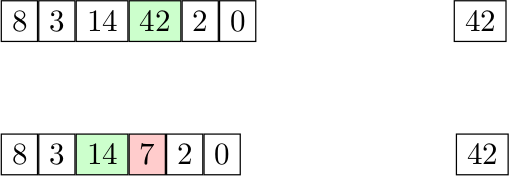
Je vous donne un tableau contenant des nombres entiers, et je vous pose une simple question : Quelle est la valeur maximale de ce tableau ? Naturellement, on peut parcourir tous les éléments et les comparer afin de trouver le maximum, cet algorithme naïf a une complexité linéaire en \(O(N)\) avec \(N\) la taille du tableau. Mais maintenant, je décide de changer quelques valeurs dans le tableau et je vous repose la question. On peut à nouveau parcourir tout le tableau, et comparer nos \(N\) éléments pour chercher le maximum, mais peut-on faire mieux ? Une des premières idées qui peut vous venir à l'esprit serait d'utiliser une variable en plus du tableau qui contient le maximum actuel, on l'initialise avec le maximum qu'on a trouvé en parcourant le tableau, et ensuite dès qu'on effectue une modification on compare cette variable aux valeurs que l'on change pour la mettre à jour. Cependant cette méthode, qui peut paraitre bien au premier coup d'œil, ne fonctionne pas dans tous les cas. Si la valeur que l'on change dans le tableau est l'ancien maximum (et donc la valeur de notre variable externe), alors il se peut que le nouveau maximum ne soit plus la valeur qu'on a changée mais une autre contenue dans le reste du tableau :

Dans cet exemple, on part du tableau 8, 3, 14, 42, 2, 0 qu'on a parcouru et dont on a retenu la valeur maximale (en vert) dans notre variable à part : 42. Cependant, quand on change le maximum actuel par un nombre plus petit (7 dans notre cas), la variable externe ne change pas puisque 7 < 42 alors que le maximum du tableau n'est plus le même (c'est 14 désormais). Cet algorithme est donc invalide, et il nous en faut un nouveau pour trouver rapidement le maximum d'un tableau dynamique.
Une autre idée serait de diviser notre gros problème en plus petits sous problèmes. Au lieu de se demander quel est le maximum de tout le tableau, on peut commencer par se demander quel est le maximum entre les deux premiers éléments du tableau, puis entre les deux suivants, etc. Une fois qu'on a tous ces maximums, on a divisé le nombre d'éléments à visiter par deux pour répondre à notre problème initial puisque désormais on peut simplement parcourir les maximums locaux pour trouver le maximum du tableau. Mais on peut continuer de diviser notre problème, en trouvant les maximums des maximums, etc. jusqu'à arriver à la valeur maximale contenue dans le tableau.
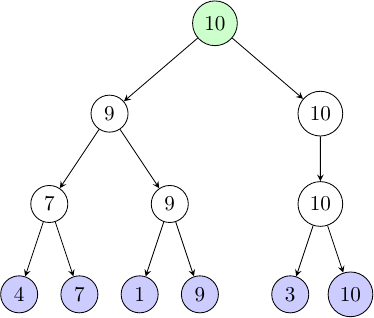
Les éléments en bleus représentent notre tableau initial, et l'élément en vert est le maximum du tableau trouvé grâce à notre méthode. On commence en bas avec notre tableau, et on monte progressivement en prenant à chaque fois les maximums deux à deux. Cette structure s'apparente à un arbre, mais a la particularité de ne pas posséder plus de deux fils par nœud (car on compare les éléments deux à deux à chaque fois). Cette propriété nous permet de démontrer qu'il suffit dans le pire des cas \(log _2 N\) changements (en savoir plus sur les logarithmes) pour modifier le maximum du tableau (et donc la racine de l'arbre). C'est-à-dire que lorsqu'on modifie des valeurs, il suffit uniquement de modifier les pères des nœuds affectés, et de simplement remonter petit à petit à la racine en recalculant uniquement les maximums locaux nécessaires. Or, la hauteur de cet arbre est dans le pire des cas de \(log _2 N\), notre algorithme a donc une complexité en \(O(\log _2 N)\) pour trouver le maximum d'un tableau dynamique.
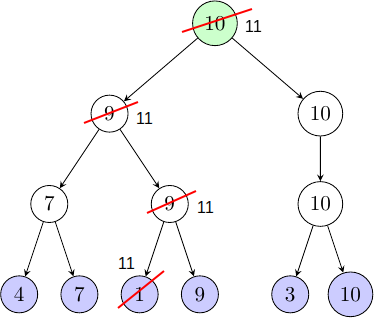
Pour changer une valeur dans notre tableau (ici le 1 devient un 11), on change aussi les nœuds de l'arbre en remontant tant que le maximum local a changé.
Cette structure de données porte un nom : un arbre binaire (et plus particulièrement un arbre binaire maximal dans notre cas), et elle est très utile dans le domaine de la recherche, mais nous verrons que son utilisation ne se limite pas à cette catégorie d'algorithme et qu'elle est présente dans de nombreux autres structures de données plus complexes.
Un arbre binaire (ou binary tree en anglais) est un type d'arbre spécifique avec comme contrainte de ne pas avoir plus de deux fils par nœuds. On appelle alors les deux fils d'un nœud le fils gauche et le fils droit.
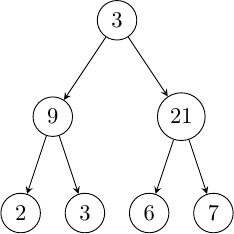
Cette structure de données a l'avantage d'être très modulable et on peut lui appliquer différentes propriétés afin d'en changer son comportement, en voici quelques-unes :
Dans un arbre binaire, ajouter et supprimer un élément est relativement simple, il suffit uniquement de respecter les propriétés de l'arbre utilisé. Dans notre cas, on utilise un arbre binaire normal :

Ajouter un nœud suit une logique, on cherche à ne pas faire de "trous" dans notre arbre binaire, et on va donc combler tant que possible les espaces vides dans l'ordre (les nœuds en verts représentent le nouveau nœud à chaque étape).
Pour la suppression d'un nœud, il y a trois cas possibles :
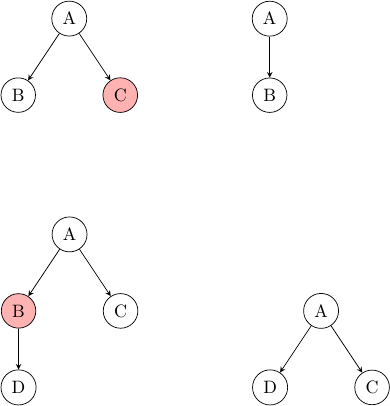
Dans le premier cas, C est une feuille, il n'y a donc aucuns soucis pour le supprimer. Dans le deuxième cas, B a un fils D, lorsqu'on supprime B on le remplace donc par D.
Dès qu'un arbre binaire possède des propriétés, les opérations d'insertion et de suppression sont différentes. Elles peuvent être plus ou moins complexes en fonction des propriétés ajoutées à l'arbre binaire, mais doivent être bien définies pour avoir une structure opérationnelle. D'autres opérations peuvent être utiles sur certains arbres binaires, par exemple la possibilité de changer une valeur dans un tableau (ce qui implique souvent des changements dans l'arbre en lui-même). Le parcours d'un arbre binaire peut aussi évoluer en fonction de ses caractéristiques, et même s'il reste un arbre, parfois il faut adapter sa méthode de parcours pour utiliser le mieux possible la structure de données.
Même s'il est très rare de devoir implémenter un simple arbre binaire sans aucunes propriétés, savoir le représenter est important, car c'est en fonction de cette représentation que l'on peut ensuite construire des opérations spécifiques à la structure. Un arbre binaire n'est techniquement qu'une structure dérivée de l'arbre, on peut donc l'implémenter de la même façon que ce dernier, mais vu les contraintes de cette structure de données, il est possible d'utiliser d'autres manières.
Les possibilités d'implémentation d'un arbre ne s'appliquent pas forcément bien pour un arbre binaire, en effet, on sait qu'il n'aura qu'au maximum deux fils, on peut donc simplement utiliser une structure auto référentielle :
typedef struct Noeud Noeud;
struct Noeud
{
Noeud *gauche;
Noeud *droit;
int donnee;
};
typedef Noeud *ArbreBinaire;Chaque nœud pointe alors vers ses deux fils, reliant ainsi les éléments entre eux pour former notre arbre binaire. Cette solution permet un stockage optimal en mémoire, ainsi qu'une facilité pour insérer et supprimer des éléments, mais elle peut être un inconvénient lorsqu'on a besoin d'accéder rapidement à des éléments (en effet, il faut parcourir l'arbre jusqu'à un élément particulier pour récupérer ses données).
Une autre implémentation consiste à utiliser un simple tableau, permettant un accès rapide en \(O(1)\) à n'importe quel élément, mais qui est moins souple que la dernière solution. On l'utilise notamment pour construire des arbres binaires min ou max, car on n'a pas besoin de modifier d'autres nœuds que des feuilles dans ces derniers, et on veut souvent accéder à la racine rapidement.
Pour stocker notre arbre binaire, on va prendre chaque élément de l'arbre profondeur par profondeur (de gauche à droite), et les placer dans le tableau dans cet ordre.
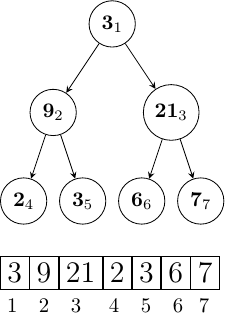
Ce tableau permet notamment un accès rapide, et un parcours facile grâce à sa manière de stocker les nœuds qui nous renseigne sur qui est le père/fils gauche/fils droit d'un nœud :
Ce tableau suffit donc à stocker un arbre binaire :
int arbreBinaire[NB_NOEUD_ARBRE + 1];On n'oublie pas d'allouer une case de plus dans notre tableau car la racine doit obligatoirement être l'élément d'indice 1 du tableau pour satisfaire les propriétés de placement des nœuds.
Cela peut paraitre étrange de penser qu'un simple arbre avec une contrainte sur le nombre de nœuds de ses fils peut être extrêmement utile. Et pourtant, les arbres binaires sont présents dans énormément d'algorithmes et de structures de données, et en voici une courte liste :
La liste des applications d'un arbre binaire peut continuer longtemps, car cette structure de données est fondamentale en algorithmique. Son principe est simple, son implémentation aussi, mais ses applications peuvent être très complexes.