Tri par tas

Introduction

Le tri par tas (heapsort en anglais) est un algorithme de tri par comparaison, plutôt efficace et qui a une complexité en \(O(N \log _2 N)\). C’est un algorithme de tri non stable mais en place.

Principe de l’algorithme

L'algorithme du tri par tas repose sur un élément fondamental : le tas (d'où son nom). En effet, ce tri crée un tas max du tableau donné en entrée, et le parcourt afin de reconstituer les valeurs triées dans notre tableau.

Exemple

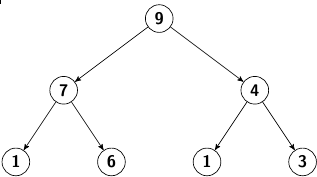
On prend la suite de nombres suivante que l’on va trier dans l’ordre croissant avec le tri par tas : 1, 9, 3, 7, 6, 1, 4.

1ère étape : créer le tas (max dans notre cas)

2ème étape : parcourir le tas pour trier les éléments

Pour trier les éléments grâce à notre tas, on retire la racine à chaque tour (l'élément le plus grand de notre tas, et donc de notre tableau), on le range à sa place définitive, et on entasse le dernier élément du tas pour combler le trou de la racine mais aussi respecter les règles d'un tas.

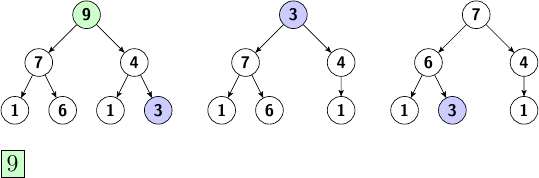
La racine du tas (en vert) est placée dans le tableau (1) et le dernier élément (en bleu) va remplacer la racine (2), mais il ne faut pas oublier de l'entasser pour respecter les règles du tas max (3).

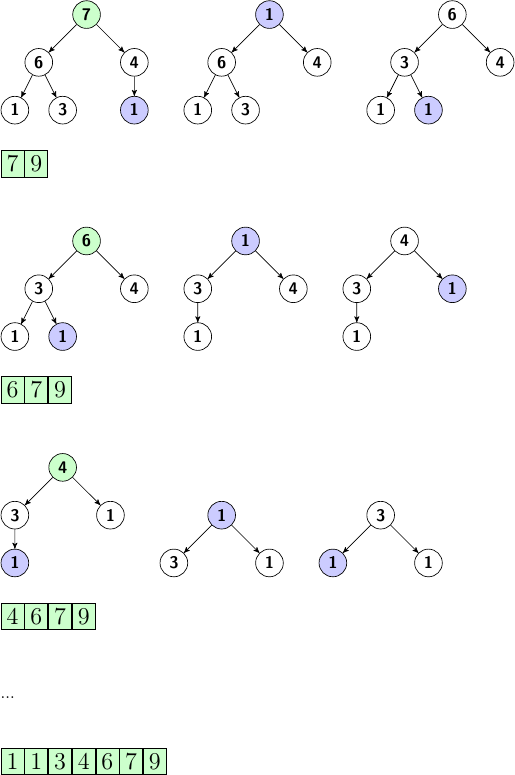
On continue ces opérations tant que le tas contient des éléments :

Pseudo-code

Voici le pseudo-code du tri par tas :

triTas :

   Contruire le tas max du tableau

   Pour chaque élément du tableau (en partant de la fin)
      Placer la racine du tas dans le tableau
      Entasser le dernier élément du tas à la place de la racine

Complexité

La complexité de l’algorithme du tri par tas est en \(O(N \log _2 N)\). En effet, la boucle principale parcourt \(N\) tours (\(N\) étant la taille du tableau), et appelle à chaque tour une fonction pour entasser qui a une complexité logarithmique.

Si vous n’avez pas lu mon article sur le `tri rapide </algo/tri/tri_rapide.html>`__, je vous conseille au moins de lire la partie `complexité </algo/tri/tri_rapide.html#complexite>`__ dans laquelle j’explique pourquoi le tri rapide peut être jusqu’à deux fois plus efficace que le tri par tas.

Implémentation

Une implémentation en C++ (afin d'avoir le type priority_queue) du tri par tas :

#include <cstdio>
#include <queue>
using namespace std;

const int TAILLE_MAX = 1000;

int tableau[TAILLE_MAX];
int taille;

priority_queue <int> tas;

void construireTasMax(void)
{
   int iTab;
   for(iTab = 0; iTab < taille; ++iTab)
      tas.push(tableau[iTab]);
}

void triTas(void)
{
   int iTab;

   construireTasMax();

   for(iTab = taille - 1; iTab != 0; --iTab) {
      tableau[iTab] = tas.top();
      tas.pop();
   }
}

int main(void)
{
   int iTab;

   scanf("%d\n", &taille);

   for(iTab = 0; iTab < taille; ++iTab)
      scanf("%d ", &tableau[iTab]);

   triTas();

   for(iTab = 0; iTab < taille; ++iTab)
      printf("%d ", tableau[iTab]);
   printf("\n");

   return 0;
}

Notre tableau d'entrée :

7
1 9 3 7 6 1 4

La sortie du programme :

1 1 3 4 6 7 9

Améliorations et variantes

Optimisation de la mémoire

On peut économiser de la mémoire en évitant de créer un tas à part entière du tableau. En effet, on peut tout simplement réorganiser notre tableau afin de le parcourir comme un tas max, et ensuite il suffit de recréer les fonctions du tas à la main (construireTasMax, entasser, etc.) pour faire nos opérations dessus. Le tas aura une taille virtuelle qui occupe initialement toute la place du tableau, mais diminue progressivement au fur et à mesure que les racines du tas sont fixées à leurs places définitives dans le tableau trié.

triTas :

   Contruire le tas max dans le tableau

   Pour chaque élément du tableau (en partant de la fin)
      Échanger l'élément actuel avec la racine
      Décrémenter la taille du tas
      Entasser l'élément placé à la racine

On parcourt le tableau à l'envers afin d'échanger la racine actuelle avec l'élément occupant sa place définitive.

Mélange d'algorithme

Comme pour le tri rapide, le tri par tas peut être mélangé avec un autre algorithme de tri lorsque le tableau possède peu d’éléments afin de le rendre plus efficace. Pour en savoir plus à ce sujet, je vous invite à lire la partie mélange d'algorithme de mon article sur le tri rapide.

Smoothsort

Le smoothsort est une variante du tri par tas permettant d'améliorer la complexité en temps dans le meilleur des cas en \(O(N)\) (lorsque les nombres en entrée sont déjà triés ou quasi triés par exemple). Ce tri est assez complexe, et même s'il a une meilleure approche d'un point de vue théorique, il sera peu utilisé en pratique, tout comme le tri par tas comparé au tri rapide.

Le principe du smoothsort est de baser le tri non plus sur un seul tas, mais sur plusieurs de différentes tailles. Cette nouvelle structure de données est un tas de Léonard, car elle s'appuie sur la suite de Léonard.

Cet ensemble a des propriétés spécifiques (sur la taille des sous-arbres, l'ordre d'apparition des racines, etc.), rendant les opérations d'insertion et de suppression assez longues à décrire et à expliquer. Il faudrait un article à part entier pour évoquer ce curieux algorithme de tri, et si ce dernier vous intéresse je vous recommande fortement cette page qui traite en profondeur du sujet : Smoothsort Demystified.

Conclusion

Le tri par tas est donc un algorithme de tri efficace en \(O(N \log _2 N)\) non stable mais en place. En pratique, cet algorithme est moins utilisé que le tri rapide, même si en théorie il a une meilleure complexité dans le pire des cas ainsi qu'une amélioration intéressante : le smoothsort. Il sert en revanche à l'amélioration du tri rapide, dans sa variante l'introsort et reste donc un algorithme de tri essentiel à connaître.