Tri rapide

Introduction

Le tri rapide (quicksort en anglais) est un algorithme de tri par comparaison, son fonctionnement est plutôt simple à comprendre et il est très utilisé sur de grandes entrées. En effet, il a pour complexité moyenne \(O(N \log _2 N)\) et \(O(N^2)\) dans le pire des cas. Cependant, même si cet algorithme est lent dans le pire des cas, il est plus utilisé en pratique que d’autres tris comme le tri par fusion qui a une complexité dans le pire des cas en \(O(N \log _2 N)\). C’est un algorithme non stable mais en place.

Principe de l’algorithme

Le tri rapide utilise le principe de diviser pour régner, c’est-à-dire que l’on va choisir un élément du tableau (qu’on appelle pivot), puis l’on réorganise le tableau initial en deux sous tableaux :

• L’un contenant les éléments inférieurs au pivot.
• L’autre contenant les éléments supérieurs au pivot.

On continue ce procédé (qu'on appelle partitionnement, c'est-à-dire choisir un pivot et réorganiser le tableau) jusqu’à se retrouver avec un tableau découpé en \(N\) sous tableaux (\(N\) étant la taille du tableau), qui est donc trié.

Exemple

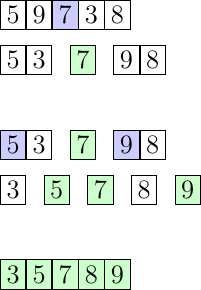
Prenons 5, 9, 7, 3, 8 comme suite de nombres, et trions la dans l'ordre croissant avec l'algorithme du tri rapide :

5, 9, 7, 3, 8 -> on choisit le pivot, dans notre cas je choisis l'élément du milieu, 7.

5, 3 | 7 | 9, 8 -> on découpe le tableau en trois parties, une partie avec des éléments inférieurs au pivot (5 et 3), la partie contenant le pivot (7), et une partie avec les éléments supérieurs au pivot (9 et 8). On peut déjà dire qu'on a placé le pivot à sa place définitive dans le tableau, puisque les autres éléments sont soit supérieurs soit inférieurs à lui.

5, 3 | 7 | 9, 8 -> on recommence en choisissant de nouveau un pivot pour chaque sous tableaux créés.

3 | 5 | 7 | 8 | 9 -> dernière étape du partitionnement, désormais aucuns sous tableaux ne contient plus d'un élément, le tri est donc terminé.

3, 5, 7, 8, 9

Sur cette image, à chaque tour on choisit notre pivot (en bleu), on sépare notre tableau en trois parties en réorganisant les éléments selon le pivot (qui est désormais bien placé et en vert), puis on recommence l'opération. À la fin du deuxième tour, nos sous tableaux qui ne sont pas des pivots (en blanc) ne contiennent plus qu'un seul élément, ils sont donc triés, comme le reste du tableau.

Pseudo-code

Voici le pseudo-code du tri rapide :

triRapide (début, fin) :

   Si le tableau a un seul élément
      Arrêter
   Sinon
      Choisir le pivot
      Réorganiser le tableau selon notre pivot

      triRapide(début, pivot - 1)
      triRapide(pivot + 1, fin)

On utilise le principe de récursivité pour implémenter notre tri rapide (comme pour le tri fusion). Les appels récursifs s'arrêtent quand le sous tableau actuel n'a plus qu'un seul élément, sinon on partitionne notre tableau (choix du pivot et réorganisation), puis on recommence l'opération sur les deux parties du tableau ne contenant pas le pivot (la partie où les éléments lui sont inférieurs, et la partie où ils sont supérieurs).

Complexité

Le calcul de la complexité du tri rapide est très semblable à celui du tri par fusion, sauf qu'au lieu de fusionner nos sous tableaux, on les réorganise (mais cette opération est de nouveau en temps linéaire, comme pour la fusion de deux sous tableaux), on retrouve aussi les deux appels récursifs qui divisent par deux notre tableau actuel. La complexité est donc calculée de la même façon, et on se retrouve bien avec un résultat en \(O(N \log _2 N)\).

Il faut savoir que le tri rapide peut s'exécuter deux fois plus vite que le tri par tas pour des raisons de mémoire cache. Les deux algorithmes ont la même complexité en moyenne, mais le tri par tas compare en général des éléments du tableau qui sont assez éloignés contrairement au tri rapide. Or, quand vous accédez à un tableau, votre ordinateur place une certaine partie de ce tableau (ou la totalité) dans une mémoire cache pour que l'accès à ce dernier se fasse plus rapidement. Dans le cas de très grandes entrées, le tri par tas va obliger la mémoire à charger et décharger successivement des parties du tableau (trop grand pour être entièrement stocké dans la mémoire cache), ce qui ralentira l'exécution du programme.

Implémentation

L’implémentation en C du tri rapide :

#include <stdio.h>

#define TAILLE_MAX 1000

int tableau[TAILLE_MAX];
int taille;

void echanger(int index1, int index2)
{
   int temp;

   temp = tableau[index1];
   tableau[index1] = tableau[index2];
   tableau[index2] = temp;
}

void triRapide(int debut, int fin)
{
   int iTab;
   int dernierEmplacement;

   if(debut >= fin)
      return;

   echanger(debut, (debut + fin) / 2);
   dernierEmplacement = debut;

   for(iTab = debut + 1; iTab <= fin; ++iTab) {
      if(tableau[iTab] < tableau[debut]) {
         ++dernierEmplacement;
         echanger(dernierEmplacement, iTab);
      }
   }

   echanger(debut, dernierEmplacement);

   triRapide(debut, dernierEmplacement - 1);
   triRapide(dernierEmplacement + 1, fin);
}

int main(void)
{
   int iTab;

   scanf("%d\n", &taille);

   for(iTab = 0; iTab < taille; ++iTab)
      scanf("%d ", &tableau[iTab]);

   triRapide(0, taille - 1);

   for(iTab = 0; iTab < taille; ++iTab)
      printf("%d ", tableau[iTab]);
   printf("\n");

   return 0;
}

L'entrée :

5
5 9 7 3 8

Notre tableau trié en sortie :

3 5 7 8 9

En C, qsort est une implémentation du tri rapide définie dans stdlib.h. En C++, il vous suffit d'inclure cstdlib pour pouvoir l'utiliser.

Améliorations et variantes

Choix du pivot

Le pivot est l'élément central du tri rapide, et le choix de ce dernier peut faire la différence entre une bonne et une mauvaise implémentation. Le choix optimal de pivot serait la médiane du tableau car cette dernière permettrait de couper de manière égale le tableau, surtout qu'il est possible de trouver cette médiane en temps linéaire grâce à l'algorithme médiane des médianes.

Par exemple avec ce tableau : 3, 9, 7, 5, 1 si l’on prend comme dans les exemples notre pivot au milieu (soit 7), on se retrouve avec les deux sous tableaux suivants : 1, 3, 5 et 9 qui ne sont pas de la même taille. En revanche, si l’on prend 5 comme pivot (la médiane du tableau), on se retrouve avec les deux sous tableaux : 1, 3 et 7, 9 qui contiennent deux éléments chacun.

Le fait que nos sous tableaux soient de la même taille (ou environ de la même taille), permettrait de diminuer le nombre d'appels récursifs de la fonction et améliorer ainsi notre complexité en temps. Cette économie d'appels récursifs peut paraitre mineure sur de petites entrées, mais peut vraiment faire une grosse différence sur d'importants tableaux. Techniquement, avec cette amélioration, notre implémentation du tri rapide a une complexité dans le pire des cas en \(O(N \log _2 N)\).

Mélange d'algorithme

Il faut savoir que le tri rapide peut s'exécuter plus lentement sur de petites entrées que des algorithmes en temps quadratique comme le tri par sélection, ou le tri par insertion (qui eux sont moins efficaces sur des entrées de grande taille).

On peut donc combiner les deux tris, et faire en sorte d’utiliser le tri par insertion (ou par sélection) lorsque la taille du tableau est inférieure à une certaine limite. Cette taille limite varie en général entre 15 et 30 éléments, mais peut changer selon l’ordinateur utilisé et l'implémentation des deux tris.

Introsort

Dans le même genre que d'utiliser un algorithme quadratique sur de petites entrées, l'introsort utilise un mix de tri rapide et de tri par tas afin de contrer un problème de lenteur dû au nombre d'appels récursifs importants du tri rapide. Une fois que ce nombre a dépassé une certaine limite, le travail est assuré par le tri par tas pour améliorer le temps d'exécution et ne pas exploser la pile d'appel. Grâce à cela, notre temps d'exécution dans le pire des cas est de \(O(N \log _2 N)\).

Conclusion

Le tri rapide est donc un algorithme de tri efficace, qui a une complexité en \(O(N \log _2 N)\) et \(O(N^2)\) dans le pire des cas (ce qui est assez rare en pratique, et peut être amélioré). Cependant, cet algorithme est très utilisé de nos jours grâce à sa rapidité (jusqu'à deux fois plus rapide que le tri par tas pour des raisons de cache, et dans la plupart du temps plus efficace que le tri fusion grâce à ses améliorations). Cet algorithme est aussi utilisé comme fonction de tri de base dans les librairies standards (comme en C ou en C++).