Le tri par insertion (insertion sort en anglais) est un algorithme de tri par comparaison simple, et intuitif mais toujours avec une complexité en \(O(N^2)\). Vous l’avez sans doute déjà utilisé sans même vous en rendre compte : lorsque vous triez des cartes par exemple. C’est un algorithme de tri stable, en place, et le plus rapide en pratique sur une entrée de petite taille.
Le principe du tri par insertion est de trier les éléments du tableau comme avec des cartes :
Prenons comme exemple la suite de nombre suivante : 9, 2, 7, 1 que l’on veut trier en ordre croissant avec l’algorithme du tri par insertion :
1er tour :
9 | 2, 7, 1 -> à gauche la partie triée du tableau (le premier élément est considéré comme trié puisqu'il est seul dans cette partie), à droite la partie non triée. On prend le premier élément de la partie non triée, 2, et on l'insère à sa place dans la partie triée, c'est-à-dire à gauche de 9.
2ème tour :
2, 9 | 7, 1 -> on prend 7, et on le place entre 2 et 9 dans la partie triée.
3ème tour :
2, 7, 9 | 1 -> on continue avec 1 que l’on place au début de la première partie.
1, 2, 7, 9
Pour insérer un élément dans la partie triée, on parcourt de droite à gauche tant que l'élément est plus grand que celui que l'on souhaite insérer.
Pour résumer l'idée de l'algorithme :

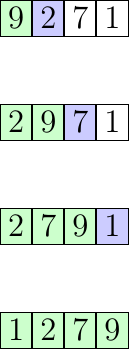
La partie verte du tableau est la partie triée, l'élément en bleu est le prochain élément non trié à placer et la partie blanche est la partie non triée.
triInsertion :
Pour chaque élément non trié du tableau
Décaler vers la droite dans la partie triée, les éléments supérieurs à
celui que l'on souhaite insérer
Placer notre élément à sa place dans le trou ainsi crééL’algorithme du tri par insertion a une complexité de \(O(N^2)\) :
Dans le pire des cas on parcourt \(N^2\) tours, donc le tri par insertion a une complexité en temps de \(O(N^2)\).
L’implémentation en C du tri par insertion :
#include <stdio.h>
#define TAILLE_MAX 1000
int tableau[TAILLE_MAX];
int taille;
void triInsertion(void)
{
int iTab;
for(iTab = 0; iTab < taille; ++iTab) {
int aInserer;
int position;
aInserer = tableau[iTab];
position = iTab;
while(position > 0 && aInserer < tableau[position - 1]) {
tableau[position] = tableau[position - 1];
--position;
}
tableau[position] = aInserer;
}
}
int main(void)
{
int iTab;
scanf("%d\n", &taille);
for(iTab = 0; iTab < taille; ++iTab)
scanf("%d ", &tableau[iTab]);
triInsertion();
for(iTab = 0; iTab < taille; ++iTab)
printf("%d ", tableau[iTab]);
printf("\n");
return 0;
}L'entrée du tri :
4
9 2 7 1Et en sortie, notre tableau trié :
1 2 7 9Le tri par insertion doit décaler de nombreuses fois le tableau pour insérer un élément, ce qui est une opération lourde et inutile puisqu'on peut utiliser des listes chaînées afin de contrer ce problème. Les listes chaînées permettent d'insérer notre élément de façon simple et plus rapide, cependant comme il faut toujours calculer où placer cet élément, la complexité reste quadratique.
Le tri par insertion est un algorithme de tri très efficace sur des entrées quasiment triées, et on peut utiliser cette propriété intéressante du tri pour l'améliorer. En effet, le tri Shell (Shell sort en anglais, du nom de son inventeur Donald L. Shell) va échanger certaines valeurs du tableau à un écart bien précis afin de le rendre dans la plupart des cas presque trié. Une fois qu'on a ce tableau ré-arrangé, on lui applique notre tri par insertion classique, mais ce dernier sera bien plus rapide grâce à notre première étape.
Pour calculer cet écart, on utilise cette formule :
Par exemple, on souhaite trier la suite de nombres : 5, 8, 2, 9, 1, 3 dans l'ordre croissant :
On calcule les écarts tant que le résultat est inférieur à la taille du tableau.
On a donc deux écarts que l'on peut utiliser : 1 et 4 (13 étant supérieur au nombre d'éléments du tableau). Cependant appliquer un écart de 1 revient à faire un tri par insertion normal, on utilisera donc uniquement l'écart de 4 dans cet exemple.
On compare ensuite chaque élément du tableau écarté de quatre éléments :
On répète cette opération tant qu'il nous reste des écarts, dans notre cas c'est la fin de la première étape du tri. Maintenant notre tableau est réorganisé et quasi trié, on peut donc lui appliquer un tri par insertion.
Malheureusement, le tri Shell reste avec une complexité quadratique dans le pire des cas, mais est une bonne amélioration de manière général.
Le tri par insertion est basé sur le fait que le tableau est coupé en deux parties, l’une triée (celle qui nous intéresse) et l’autre non triée. On peut améliorer la recherche de l'emplacement où insérer notre élément grâce à la dichotomie (c’est un algorithme de recherche efficace dans un ensemble d’objet déjà trié, ce qui est parfait pour notre cas).
Cette recherche consiste à utiliser la méthode du diviser pour régner, on cherche l’emplacement pour notre élément à l’aide d’intervalles. Notre intervalle de départ est : début partie triée -> fin partie triée :
Une fois que l’intervalle ne contient plus qu’un seul élément, on a trouvé l’emplacement où insérer l'élément à sa place. Grâce à cette amélioration, l’algorithme du tri par insertion a pour complexité \(O(N \log _2 N)\).
J'ai expliqué ici très rapidement le principe de la dichotomie, j'en parle plus longuement dans mon article à ce propos donc si vous n'avez pas tout suivi, je vous conseille d'aller le lire pour bien saisir ce concept fondamental en algorithmie.
L'algorithme du tri par insertion est simple et relativement intuitif, même s'il a une complexité en temps quadratique. Cet algorithme de tri reste très utilisé à cause de ses facultés à s'exécuter en temps quasi linéaire sur des entrées déjà triées, et de manière très efficace sur de petites entrées en général (souvent plus performant, dans ce cas, que des algorithmes de tri en \(O(N \log _2 N)\)).