
Si je vous donne un annuaire téléphonique contenant plusieurs milliers de coordonnées, et que je vous demande de trouver une personne, normalement en quelques secondes vous y arrivez. Même si je rajoute plusieurs millions de personnes dans l'annuaire, vous devriez toujours être capable de repérer n'importe qui en moins d'une minute. Mais comment faire pour qu'un ordinateur nous remplace pour effectuer cette tâche ? Comment concrétiser l'algorithme que vous utilisez (sans le savoir) pour qu'un ordinateur le comprenne ? Votre cerveau est un outil incroyable qui n'aime pas faire des actions répétitives, et il essaiera naturellement de trouver une façon plus rapide de résoudre un problème. Vous n'auriez pas idée de commencer par regarder toutes les personnes avec un prénom en "A" si vous savez que la personne que vous cherchez est "Jean". Ce que vous faites plutôt, c'est que vous divisez l'intervalle de recherche à partir d'un résultat, vous ouvrez par exemple une page au hasard qui devrait correspondre à peu près à la lettre que vous cherchez, et vous affinez au fur et à mesure en fonction du mot de la page. Votre méthode se base sur une caractéristique très importante de votre annuaire : il est trié par ordre alphabétique.
Jouons à un petit jeu appelé le plus ou moins. Je choisis un nombre entre 1 et 100 et vous devez le deviner en moins de coup possible. À chaque fois que vous me dites un nombre, je vous dis si ce dernier est supérieur ou inférieur à celui que j'ai choisi (ou égal si vous avez trouvé).
Vu comme ça, on pourrait se dire qu'on a 1 chance sur 100 de tomber sur le bon nombre, mais en réfléchissant bien on peut améliorer nos chances en s'aidant de la réponse que je donne à chaque fois (si c'est plus ou moins). Je choisis donc mon nombre, et au premier tour vous dites 50, si je vous dis « plus » vous savez que mon nombre sera forcément dans l'intervalle de 51 à 100, si je vous dis « moins » il sera dans l'intervalle 1 à 49, et si je vous dis égal vous avez trouvé le nombre. On peut continuer d'utiliser ce principe pour diviser par deux à chaque fois notre intervalle de recherche jusqu'à avoir un seul élément dans notre intervalle, qui est forcément celui que j'ai choisi au début du jeu. Cette méthode s'appelle la dichotomie, et vous utilisez un algorithme très similaire lorsque vous recherchez une personne dans un annuaire, mais elle ne s'applique pas qu'à cela, et on la retrouve dans bien d'autres domaines.
La dichotomie (binary search en anglais), est un algorithme de recherche efficace pour trouver un nombre dans un ensemble trié (ce point est très important puisque l'algorithme repose dessus). La dichotomie utilise le principe du diviser pour régner afin de découper notre problème initiale en un sous problème plus petit.
On commence toujours la dichotomie dans un intervalle de recherche, puis à chaque étape on compare notre élément qu'on cherche à l'élément central de l'intervalle :
À chaque tour, on actualise notre intervalle de recherche et on recommence les opérations tant qu'on n'a pas trouvé notre élément.
Prenons un tableau trié : 1, 8, 15, 42, 99, 160, 380, 512, 678, 952, 1304. Nous cherchons dans ce tableau l'emplacement de l'élément 512 et nous allons utiliser le principe de la dichotomie pour le trouver :
1, 8, 15, 42, 99, 160, 380, 512, 678, 952, 1304 : on compare l'élément du milieu de l'intervalle (c'est le premier tour, on commence donc par un intervalle contenant tout le tableau) avec l'élément qu'on cherche. 512 > 160, donc on peut oublier les éléments avant 160 (compris), pour se concentrer sur la partie supérieure de l'intervalle.
380, 512, 678, 952, 1304 : notre intervalle est donc divisé en deux, et on continue nos opérations. 512 < 678 donc on continue notre recherche dans la partie inférieure de l'intervalle.
380, 512 : 512 > 380, on continue dans la partie supérieure de l'intervalle.
512 : notre intervalle ne contient plus qu'un seul élément, c'est donc forcément celui qu'on recherche.
Pour résumé le principe :

L'élément en bleu est celui du milieu que l'on compare, et ensuite on choisit la bonne portion du tableau (en vert) en fonction de cette comparaison pour couper notre intervalle en deux à chaque tour.
On peut faire le pseudo-code suivant d'un algorithme de la dichotomie :
dichotomie :
Tant qu'on n'a pas trouvé l'élément
Si l'élément est supérieur au milieu
Réduire l'intervalle à la partie supérieure
Si l'élément est inférieur au milieu
Réduire l'intervalle à la partie inférieure
Sinon
Arreter la rechercheEt il est tout à fait possible d'écrire cet algorithme sous forme récursive :
dichotomie (début, fin) :
Si la recherche est supérieure au milieu
Retourner dichotomie(milieu + 1, fin)
Si la recherche est inférieure au milieu
Retourner dichotomie(debut, milieu - 1)
Sinon
Retourner l'élément au milieuPour calculer la complexité en temps de la recherche dichotomique, on peut visualiser la décomposition des intervalles grâce à un arbre :
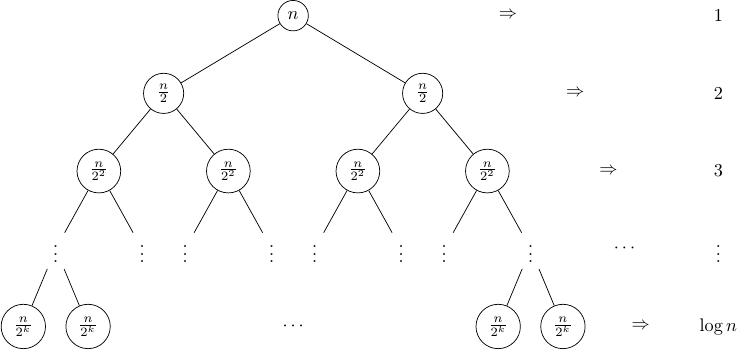
Chaque opération possible est représentée dans notre arbre, c'est-à-dire qu'à chaque tour on coupe notre tableau (qu'on note \(n\)) en deux. On voit qu'on arrive à une profondeur maximale de l'arbre en \(\log _2 N\) avec \(N\) la taille de notre tableau (pour en savoir plus sur le logarithme : lien de la page Wikipédia), la complexité de la recherche dichotomique est donc dans le pire des cas en \(O(\log _2 N)\).
Pour vous faire comprendre à quel point cette recherche est efficace, imaginons que vous possédez une bibliothèque numérique de \(N\) livres tous triés en fonction du titre par ordre alphabétique. Votre machine sur laquelle vous faites vos recherches de livres est très lente, et peut effectuer uniquement 2000 opérations à la seconde (aujourd'hui les ordinateurs classiques peuvent en effectuer plusieurs milliards...). Si vous implémentez une recherche dichotomique, il vous faudra environ plus de livres qu'il n'y a de particules dans un billion d'univers visible pour que votre machine prenne plus de temps qu'un clignement d'œil.
Dans ces implémentations, je suppose que l'élément appartient bien au tableau afin de simplifier le code et de se concentrer sur la recherche dichotomique.
L'implémentation récursive en C de la recherche :
#include <stdio.h>
#define TAILLE_MAX 1000
int tableau[TAILLE_MAX];
int taille;
int recherche;
int dichotomie(int debut, int fin)
{
int milieu;
milieu = (debut + fin) / 2;
if(recherche > tableau[milieu])
return dichotomie(milieu + 1, fin);
else if(recherche < tableau[milieu])
return dichotomie(debut, milieu - 1);
else
return milieu;
}
int main(void)
{
int iTab;
scanf("%d\n", &taille);
for(iTab = 0; iTab < taille; ++iTab)
scanf("%d ", &tableau[iTab]);
scanf("\n");
scanf("%d\n", &recherche);
printf("%d\n", dichotomie(0, taille - 1) + 1);
return 0;
}Si on donne notre tableau en entrée, ainsi que l'élément qu'on recherche :
11
1 8 15 42 99 160 380 512 678 952 1304
512On obtient bien en sortie :
8La version itérative en C :
#include <stdio.h>
#define TAILLE_MAX 1000
int tableau[TAILLE_MAX];
int taille;
int recherche;
int dichotomie(void)
{
int debut, milieu, fin;
debut = 0;
fin = taille - 1;
do
{
milieu = (debut + fin) / 2;
if(recherche > tableau[milieu])
debut = milieu + 1;
else if(recherche < tableau[milieu])
fin = milieu - 1;
else
return milieu;
} while(tableau[milieu] != recherche);
return -1;
}
int main(void)
{
int iTab;
scanf("%d\n", &taille);
for(iTab = 0; iTab < taille; ++iTab)
scanf("%d ", &tableau[iTab]);
scanf("\n");
scanf("%d\n", &recherche);
printf("%d\n", dichotomie() + 1);
return 0;
}Le tableau et l'élément recherché :
11
1 8 15 42 99 160 380 512 678 952 1304
512Et la sortie obtenue :
8En C, il existe une fonction bsearch permettant de réaliser une dichotomie.
De même, en C++, la STL (Standard Template Library) implémente des fonctions de recherche dichotomique :
Nous avons donc vu que notre dichotomie permet de chercher, de manière générale, un élément dans un ensemble d'élément trié extrêmement rapidement en \(O(\log _2 N)\). Cet algorithme s'applique très bien à des tableaux pouvant contenir différents types de données (entiers, flottants, chaînes de caractères, etc.), mais on le retrouve aussi dans plusieurs autres applications :