Le tri fusion (merge sort en anglais) est un algorithme de tri par comparaison efficace qui a pour complexité \(O(N \log _2 N)\), il se base sur le principe du diviser pour régner. Cet algorithme est stable mais ne s’exécute pas en place.
L'algorithme se compose de deux parties distinctes :
L'intérêt de diviser pour ensuite fusionner est que créer un tableau trié à partir de deux sous tableaux peut s'effectuer en temps linéaire. C'est ce point en particulier qui fait la rapidité du tri fusion.
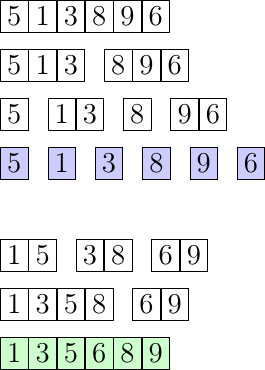
Prenons comme exemple la suite de nombre : 5, 1, 3, 8, 9, 6 que l’on veut trier avec le tri fusion dans l’ordre croissant :
1ère étape : diviser
5, 1, 3 | 8, 9, 6 -> on divise le tableau en deux.
5, | 1, 3 | 8 | 9, 6 -> on divise en deux les sous tableaux.
5 | 1 | 3 | 8 | 9 | 6 -> chaque sous tableau est de nouveau divisé pour n'avoir plus qu'un seul élément.
2ème étape : fusionner
1, 5 | 3, 8 | 6, 9 -> on prend deux sous tableaux adjacents que l'on fusionne en les ordonnant.
1, 3, 5, 8 | 6, 9 -> on continue la fusion des sous tableaux.
1, 3, 5, 6, 8, 9 -> le tableau ne contient plus de sous tableaux, il est donc trié.
1, 3, 5, 6, 8, 9
Pour résumer les deux étapes du tri :

Les éléments en bleu correspondent à l'état du tableau après la première étape, et les éléments en vert après la deuxième étape.
Voici le pseudo-code du tri fusion :
triFusion (début, fin) :
Si le tableau a un seul élément
Arrêter
Sinon
triFusion(début, milieu)
triFusion(milieu + 1, fin)
fusionner(début, milieu, fin)
fusionner (début, milieu, fin) :
A -> éléments du tableau de début à milieu
B -> éléments du tableau de milieu + 1 à fin
Pour i allant de début à fin
Si A[indexA] <= B[indexB]
Tableau[i] = A[indexA]
Incrémenter indexA
Sinon
Tableau[i] = B[indexB]
Incrémenter indexBCe pseudo-code est relativement simple :
triFusion, on utilise la récursivité
pour découper puis fusionner notre tableau, et on arrête les appels
récursifs lorsque le sous tableau que l'on traite n'a plus qu'un seul
élément.fusionner est assez explicite, elle nous
permet de créer à partir de deux sous tableaux triés, un tableau lui
aussi trié en temps linéaire.Pour démontrer la complexité du tri fusion, visualisons la découpe du
tableau réalisée dans la fonction triFusion lors des appels
récursifs :
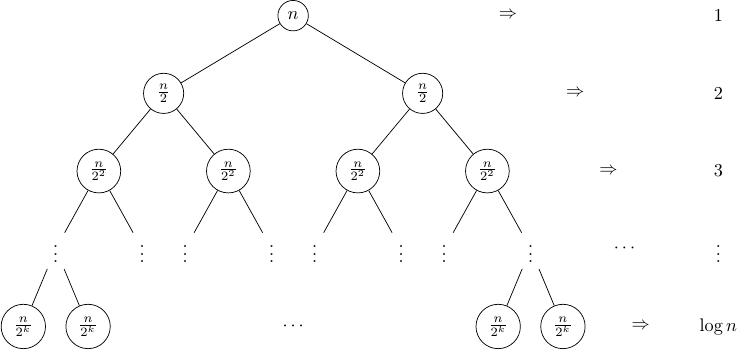
Les deux appels récursifs sont représentés par une séparation du
tableau actuel en deux, et ce qu'il faut comprendre c'est que tous les
sous tableaux d'une même profondeur formeront toujours un unique tableau
contenant \(N\) éléments (\(N\) étant la taille du tableau de départ),
puisqu'on divise par deux la taille, mais on multiplie par deux le
nombre de nœuds. C'est très important car on appelle notre fonction
fusionner à chaque nœud, or cette fonction s'exécute en
temps linéaire de \(O(N)\) avec \(N\) la taille du sous tableau. On peut donc
dire grâce aux deux dernières informations, qu'à chaque profondeur on
aura appelé notre fonction fusionner sur \(N\) éléments (quelle que soit la
profondeur). De plus, on sait que cet arbre possède \(\log _2 N\) profondeurs (pour en savoir
plus sur le logarithme : lien de la page
Wikipédia), ce qui nous donne finalement une complexité en \(O(N \log _2 N)\).
Une implémentation en C du tri fusion :
#include <stdio.h>
#define TAILLE_MAX 1000
int tableau[TAILLE_MAX];
int taille;
void fusion(int debut, int milieu, int fin)
{
int A[milieu - debut + 1];
int B[fin - milieu];
int iTab, indexA, indexB;
for(indexA = 0, iTab = debut; iTab <= milieu; ++indexA, ++iTab)
A[indexA] = tableau[iTab];
for(indexB = 0, iTab = milieu + 1; iTab <= fin; ++indexB, ++iTab)
B[indexB] = tableau[iTab];
indexA = 0;
indexB = 0;
for(iTab = debut; iTab <= fin; ++iTab) {
if(indexA == milieu - debut + 1) {
tableau[iTab] = B[indexB];
++indexB;
}
else if(indexB == fin - milieu) {
tableau[iTab] = A[indexA];
++indexA;
}
else if(A[indexA] <= B[indexB]) {
tableau[iTab] = A[indexA];
++indexA;
}
else {
tableau[iTab] = B[indexB];
++indexB;
}
}
}
void triFusion(int debut, int fin)
{
if(debut != fin) {
int milieu = (debut + fin) / 2;
triFusion(debut, milieu);
triFusion(milieu + 1, fin);
fusion(debut, milieu, fin);
}
}
int main(void)
{
int iTab;
scanf("%d\n", &taille);
for(iTab = 0; iTab < taille; ++iTab)
scanf("%d ", &tableau[iTab]);
triFusion(0, taille - 1);
for(iTab = 0; iTab < taille; ++iTab)
printf("%d ", tableau[iTab]);
printf("\n");
return 0;
}Il faut faire attention dans notre fonction fusion à
bien vérifier qu'on a encore des éléments dans les tableaux A et B avant
de les copier (si on arrive à la fin d'un des deux tableaux, on remplit
le reste avec l'autre).
L'entrée du programme :
6
5 1 3 8 9 6Et en sortie, notre tableau trié :
1 3 5 6 8 9Les listes chaînées sont effectivement un bon moyen d'implémenter le tri fusion à cause de cette flexibilité que ce tri impose. En effet, on doit pouvoir séparer des éléments pour les fusionner dans un ordre différent après, et ces opérations ne sont pas pratiques ni optimales avec des tableaux, mais sont adaptées à des listes chaînées.
La complexité en temps reste la même, mais la complexité en mémoire est améliorée.
Le tri fusion est donc un algorithme de tri efficace, qui a pour complexité \(O(N \log _2 N)\). Cependant, cet algorithme est finalement peu utilisé en pratique à cause du tri rapide qui est meilleur dans de nombreux domaines (gestion du cache, nombre de comparaisons, possibilité d'améliorations, etc.).