Le tri par sélection (selection sort en anglais) est un algorithme de tri par comparaison simple, mais assez inefficace sur une entrée trop importante, c’est un algorithme non stable mais qui trie en place. Il a pour complexité algorithmique \(O(N^2)\) comme le tri à bulles.
Le tri par sélection se décompose en deux étapes :
Le facteur qui détermine si un élément est bien placé est son rang (par exemple : le ième plus petit élément sera forcément placé en ième position du tableau). Le tri par sélection va donc à chaque tour trouver le ième plus petit élément du tableau, pour ensuite l'insérer à sa place, en commençant par le premier plus petit, et en augmentant à chaque fois (deuxième plus petit, troisième, etc.).
Prenons désormais comme exemple la suite de nombres suivante : 6, 1, 9, 3. Trions cette suite avec l’algorithme du tri par sélection dans l’ordre croissant :
1er tour :
6, 1, 9, 3 -> le plus petit élément du tableau est 1, on le place donc sur la première case (en l'échangeant avec le 6).
2ème tour :
1, 6, 9, 3 -> le deuxième plus petit élément est 3, on le place sur la deuxième case et on l’échange avec le 6.
3ème tour :
1, 3, 9, 6 -> le troisième plus petit élément est 6, on l’échange avec 9 pour le placer sur la troisième case.
4ème tour :
1, 3, 6, 9 -> le quatrième plus petit élément du tableau est 9, il est déjà en quatrième position on ne fait rien.
1, 3, 6, 9
Ce tri se décompose réellement en deux étapes distinctes :

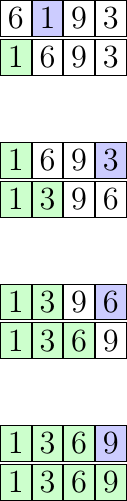
À chaque tour, on cherche le minimum dans l'espace non trié du tableau (le minimum est représenté en bleu, et la partie non triée en blanc), ensuite on déplace cet élément à sa place définitive (représentée en vert). En faisant cela pour chaque élément du tableau, ce dernier se retrouve trié au bout de \(N\) tours maximum (\(N\) étant la taille du tableau).
Le pseudo-code du tri par sélection est simple :
triSelection :
Pour chaque élément
Pour chaque élément de la partie non triée
Mettre à jour le minimum du tableau rencontré jusqu'ici
Échanger l'élément actuel avec le minimumComme pour le tri à bulles, le tri par sélection a une complexité en \(O(N^2)\) :
Sa complexité est donc légèrement inférieure à \(N^2\), cependant cette différence est mineure et sa complexité est considérée comme étant en \(O(N^2)\).
Une implémentation en C de l'algorithme du tri par sélection :
#include <stdio.h>
#define TAILLE_MAX 1000
int tableau[TAILLE_MAX];
int taille;
void echanger(int index1, int index2)
{
int temp;
temp = tableau[index1];
tableau[index1] = tableau[index2];
tableau[index2] = temp;
}
void triSelection(void)
{
int iElement, iTab;
int min;
for(iElement = 0; iElement < taille; ++iElement) {
min = iElement;
for(iTab = iElement + 1; iTab < taille; ++iTab)
if(tableau[iTab] < tableau[min])
min = iTab;
if(min != iElement)
echanger(iElement, min);
}
}
int main(void)
{
int iTab;
scanf("%d\n", &taille);
for(iTab = 0; iTab < taille; ++iTab)
scanf("%d ", &tableau[iTab]);
triSelection();
for(iTab = 0; iTab < taille; ++iTab)
printf("%d ", tableau[iTab]);
printf("\n");
return 0;
}L'entrée du programme :
4
6 1 9 3Et la sortie attendue :
1 3 6 9Tout comme pour le tri à bulles, on peut améliorer légèrement le tri par sélection pour qu'il effectue moins d'opérations. Dans notre boucle qui cherche le ième plus petit élément, on peut aussi en profiter pour chercher le jème plus grand. Grâce à cela, on divise par deux le nombre de tours que l'on réalise pour trier notre tableau, cependant, diviser par deux ne change pas la complexité finale car 2 est un facteur assez petit pour ne pas en prendre compte dans de très larges entrées. La complexité du tri reste donc quadratique.
Pour chaque élément restant
Pour chaque élément de la partie non triée
Mettre à jour le minimum et le maximum du tableau rencontré jusqu'ici
Échanger l'élément i (variant de 0 à N / 2 ) avec le minimum
Échanger l'élément j (variant de N à N / 2 ) avec le maximumDans le cas où notre tableau contient de nombreux doublons, l'algorithme de tri par sélection va effectuer plusieurs recherches de plus petits éléments sur le même élément qui n'est rien d'autre qu'un doublon. Le bingo sort permet de palier ce problème, en proposant de placer tous les éléments ayant la même valeur en même temps, sans faire de nouvelles recherches à chaque tour. Encore une fois, notre algorithme sera plus rapide en général mais pas assez pour que la complexité change, elle restera donc en \(O(N^2)\).
Pour chaque élément
Pour chaque élément de la partie non triée
Mettre à jour le minimum du tableau rencontré jusqu'ici
Pour chaque élément de même valeur que le minimum
Échanger avec l'élément actuel
Augmenter l'indice de l'élément actuelOn peut voir le tri par tas comme une amélioration directe du tri par sélection. En effet, si l'on utilise un tas pour permettre de trouver les plus petits éléments rapidement, on obtient une complexité en \(O(N \log _2 N)\) et un tri qu'on appelle tri par tas.
Le tri par sélection est donc un algorithme assez simple, mais peu efficace à cause de sa complexité en \(O(N^2)\). Cependant des améliorations et des variantes permettent de le rendre plus rapide, et le tri par sélection sert de base au tri par tas, un autre algorithme de tri bien plus efficace avec une complexité en \(O(N \log _2 N)\). Même avec une complexité quadratique, ce tri reste en pratique utilisé sur de petites entrées, mais aussi lorsqu'on a besoin d'un nombre d'échanges faible au sein du tableau (contrairement au tri par insertion qui peut être plus rapide, mais réalise plus d'échanges).