Tas

Introduction

Vous avez une liste d'éléments qui est vide au départ, et deux types d'opérations sont possibles dessus :

• Insérer une valeur dans la liste.
• Extraire le maximum (ou le minimum, le problème reste le même) de la liste.

On a vu dans l'introduction de mon article sur les arbres binaires, comment trouver le maximum dans un tableau dynamique. On pourrait utiliser la même méthode (que l'on change légèrement), et la même structure, afin d'avoir une complexité en temps efficace de \(O(\log _2 N)\). Cependant, qu'en est-il de la complexité en mémoire ? Que se passe-t-il si j'ai des milliards de milliards d'opérations ? En effet, on crée de nombreuses fois des doublons afin d'avoir notre arbre binaire maximal final, mais peut-on faire autrement ? C'est là qu'on découvre le tas, une structure permettant de faire des recherches rapides, des comparaisons efficaces, et qui prend peu de place. On peut comprendre qu'avec tous ces avantages, le tas est une structure de données énormément utilisée, importante à connaître et qui peut s'avérer très utile quand on arrive aux limites des arbres binaires max/min (ce qui est notre cas dans cet exemple).

Principe du tas

Le tas (ou heap en anglais), sera la plupart du temps implémenté comme un tas binaire, c'est-à-dire qu'il est construit sur la forme d'un arbre binaire. C'est sur cette structure que l'on va donc se concentrer dans cet article, mais sachez qu'il est possible de créer des tas basés sur des arbres autres que binaires.

Dans notre arbre binaire maximal, le père d'un nœud est le maximum des deux nœuds (autrement dit, c'est soit l'un soit l'autre), dans un tas binaire, le père d'un nœud n'est pas un double de ses enfants, mais au contraire un autre nœud indépendant qui respecte une propriété spécifique au tas (tas minimal : alors le père a une valeur inférieure ou égale à celles de ses fils, et tas maximal : le père a une valeur supérieure ou égale à celles de ses fils).

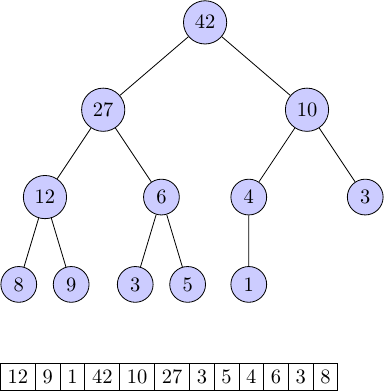
Ce tas max peut par exemple représenter le tableau situé en dessous, et le fait qu'il soit maximal nous permet de dire avec certitude que sa racine est l'élément maximum du tableau (de même un tas min aura à la racine l'élément minimum du tableau).

Opérations sur un tas

Un tas ne peut pas avoir de "trous" dedans, seul le dernier étage de l'arbre peut ne pas être rempli en entier. Lorsqu'on veut insérer un nouvel élément, on a donc pas d'autres choix que de le placer à la première place libre que l'on trouve dans le tas. Cependant, ce nouvel élément ne respecte pas les propriétés du tas, et il va falloir effectuer des modifications afin d'avoir une structure cohérente. Pour cela, on applique le même principe que lors d'un changement d'une valeur dans un arbre binaire maximal, c'est-à-dire que l'on va modifier tous les nœuds parents tant que les propriétés du tas ne sont pas respectées.

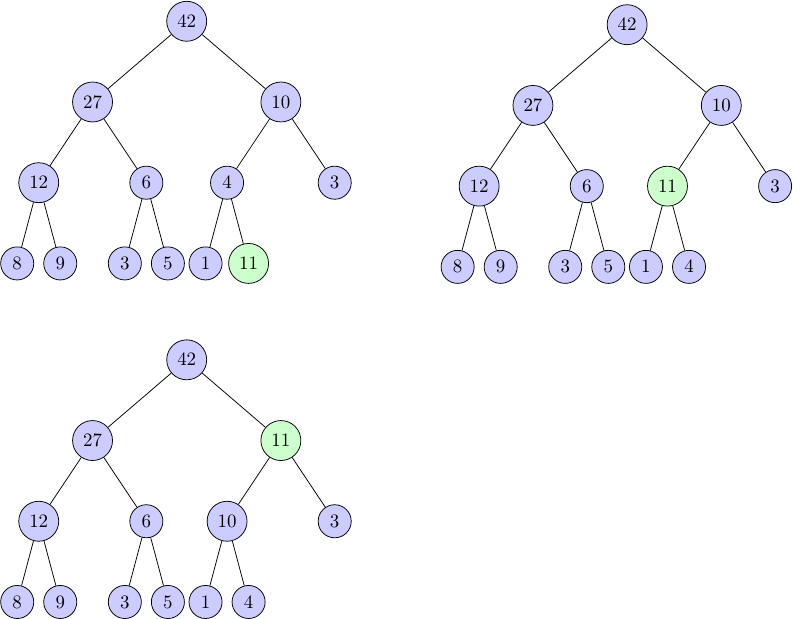
On souhaite insérer la valeur 11 (en vert) dans notre tas maximal, on le place donc sur la première place libre, puis on l'échange avec son père tant que ce dernier est plus petit que 11 (car c'est un tas maximal). À la fin, 11 a été inséré, et notre tas respecte bien les propriétés d'un tas max.

La deuxième opération principale d'un tas est l'extraction de son minimum/maximum (en fonction du tas). On a vu que cette valeur se trouve forcément à la racine, mais comment reboucher le trou qu'on vient de faire ? Une solution consiste à prendre le dernier élément du tas, et de le déplacer à la racine. Vu que c'est une feuille, on peut très bien le bouger de place sans inconvénient, cependant on ne respecte plus les propriétés du tas. On va donc entasser cet élément pour qu'il se retrouve à sa bonne place :

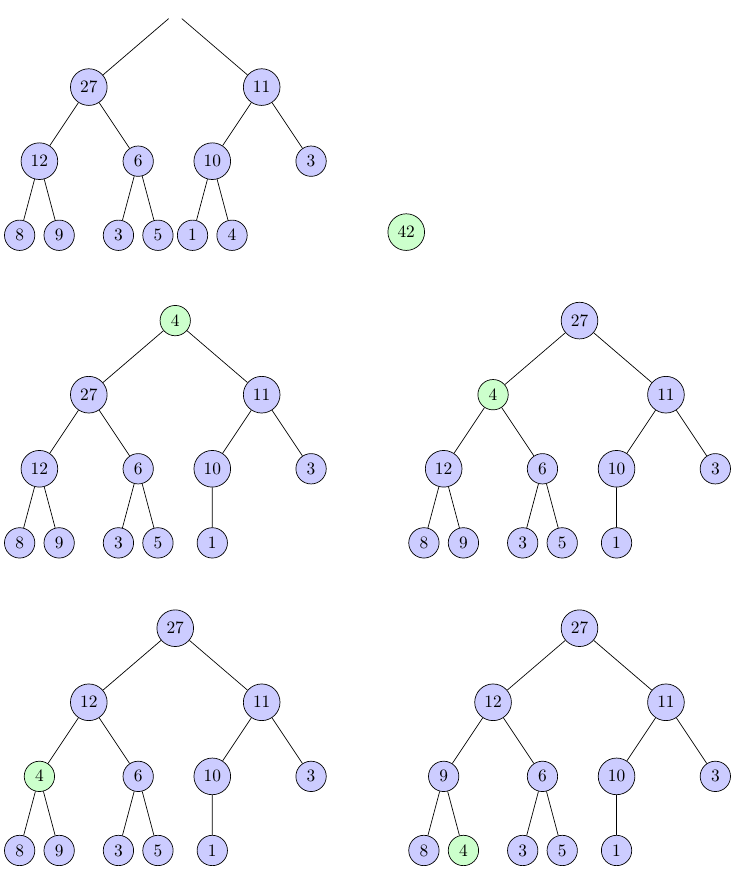
On extrait 42 qui est le maximum de notre tas, et on insère la dernière valeur à la place de la racine pour boucher le trou (c'est le 4 en vert). Pour entasser notre élément et respecter les caractéristiques d'un tas max, on échange le nœud avec le maximum de ses deux fils tant qu'on peut (pour un tas min, on échange avec le minimum de ses deux fils). Grâce à cela, on a reconstitué notre tas maximum, car le 4 est de nouveau a une place qui respecte les propriétés.

Pseudo-code

Le pseudo-code des deux opérations du tas max :

insertion (nœud) :

   Insérer le nœud à la première place disponible dans le tas

   Tant que son père est plus petit que lui
      Échanger les nœuds

extraction :

   Retirer la racine du tas

   Reboucher avec le dernier élément du tas
   Tant que le nœud n'est pas plus grand que ses deux fils
      Échanger avec le maximum de ses fils

   Retourner l'ancienne racine

Et la variante pour le tas min :

insertion (nœud) :

   Insérer le nœud à la première place disponible dans le tas

   Tant que son père est plus grand que lui
      Échanger les nœuds

extraction :

   Retirer la racine du tas

   Reboucher avec le dernier élément du tas
   Tant que le nœud n'est pas plus petit que ses deux fils
      Échanger avec le minimum de ses fils

   Retourner l'ancienne racine

Complexité

Notre tas binaire est basé sur un arbre binaire, il a donc une hauteur maximale de \(\log _2 N\) avec \(N\) le nombre d'éléments du tas. Pour l'insertion d'un élément, on fait dans le pire des cas remonter le nœud jusqu'à la racine et donc on effectue \(\log _2 N\) opérations. Pareil pour l'extraction du min/max, on fait dans le pire des cas \(\log _2 N\) échanges, résultant dans les deux cas en une complexité en \(O(\log _2 N)\).

Pour ce qui est de la complexité en mémoire, il n'y a aucuns doublons, on occupe donc uniquement l'espace nécessaire pour stocker \(N\) éléments.

Implémentation

Une implémentation en C d'un tas max :

#include <stdio.h>

#define NB_NOEUD_MAX 1000

int tas[NB_NOEUD_MAX];
int nbElement;

void echanger(int a, int b)
{
   int c;

   c = tas[a];
   tas[a] = tas[b];
   tas[b] = c;
}

int max(int a, int b)
{
   if(tas[a] > tas[b])
      return a;
   else
      return b;
}

void inserer(int valeur)
{
   int noeud, pere;

   ++nbElement;
   noeud = nbElement;
   tas[nbElement] = valeur;

   pere = noeud / 2;
   while(pere != 0 && 
         tas[noeud] > tas[pere]) {
      echanger(noeud, pere);

      noeud = pere;
      pere = noeud / 2;
   }
}

int extraire(void)
{
   int racine;
   int noeud, gauche, droit, fils;

   racine = tas[1];

   tas[1] = tas[nbElement];
   --nbElement;

   noeud = 1;
   gauche = 2;
   droit = 3;

   while(gauche <= nbElement &&
         (tas[noeud] < tas[gauche] || tas[noeud] < tas[droit])) {
      fils = max(gauche, droit);
      echanger(noeud, fils);

      noeud = fils;
      gauche = 2 * noeud;
      droit = 2 * noeud + 1;
   }

   return racine;
}

int estPuissanceDeux(int x)
{
   return (x & (x - 1)) == 0;
}

void afficher(void)
{
   int iEle;
   for(iEle = 1; iEle <= nbElement; ++iEle) {
      printf("%d ", tas[iEle]);
      if(estPuissanceDeux(iEle + 1))
         printf("\n");
   }

   printf("\n");
}

En C++, la STL (Standard Template Library) a une implémentation d'une file à priorité utilisant un tas max : priority_queue. Il est possible d'utiliser cette structure afin d'avoir un tas min, en redéfinissant l'opérateur < nous permettant de changer l'ordre de priorité dans le tas :

#include <queue>

struct Element
{
   int valeur;
   bool operator < (const Element &autre) const
   {
      if(valeur < autre.valeur)
         return false;
      else
         return true;
   }
};

priority_queue <Element> tasMin;

Variantes

Le tas possède beaucoup de variantes, certaines sont plus utiles que d'autres, et en général on choisit la plus appropriée en fonction des données que l'on reçoit, mais aussi par rapport aux opérations que l'on souhaite effectuer dessus. On peut déjà citer toutes les différentes versions du tas : binaire, ternaire, et même de façon plus globale n-aire. Il est aussi possible de découper notre tas en plusieurs sous arbres de tailles spécifiques, suivant un ordre précis, et permettant des améliorations théoriques de la complexité des opérations. Je dis bien théorique, car en pratique les implémentations ne sont pas spécialement plus rapides que des tas binaires classiques, ce sont donc des structures peu utilisées en pratique, mais qu'on peut retrouver dans certaines améliorations d'algorithmes. Les plus connus sont le tas de Fibonacci, le tas binomial, ou encore le tas jumelé mais on peut voir ce principe dans l'amélioration du tri par tas : le smoothsort. Enfin, il y a différentes variantes qui s'appuient sur l'idée d'un tas, mais la modifie afin de proposer des avantages précis pour des algorithmes ou bien des opérations, comme le tas faible qui se concentre sur le tri principalement.

Conclusion

Le tas est donc une structure de données adaptée aux opérations de recherche de minimum/maximum, et de tri. On le retrouve à la base du tri par tas, mais aussi dans la création d'une file à priorité qui elle sert dans l'algorithme de plus court chemin de Dijkstra par exemple. Des variantes de tas permettent aussi des améliorations dans plusieurs catégories d'algorithmes, et cette structure de données peut très vite créer d'autres structures complexes et puissantes avec des complexités en temps et en mémoire faibles.