L'algorithme de Dijkstra est sans doute l'un des algorithmes de plus court chemin le plus connu. Ce dernier se base sur le parcours en largeur afin de trouver le plus court chemin dans un graphe pondéré positivement (ce point est très important, mais nous y reviendrons plus en détails après). On sait qu'un parcours en largeur permet de trouver le plus court chemin sur un graphe non pondéré (où on associe chaque arc avec une longueur arbitraire de 1 unité) et qu'il utilise une file pour stocker les éléments afin de les parcourir profondeur par profondeur. L'algorithme de Dijkstra s'appuie sur la même idée, sauf qu'il ne va pas utiliser une simple file (car tous les arcs n'ont pas la même pondération) mais une file à priorité. Cette dernière permet de toujours avoir le nœud avec la distance minimale par rapport au départ en tête de file, et garantie alors qu'on a trouvé le plus court chemin lorsqu'on atteint le nœud de sortie. La file à priorité a aussi l'avantage d'être une structure de données très efficace et rapide, ce qui rend notre algorithme d'autant plus intéressant.
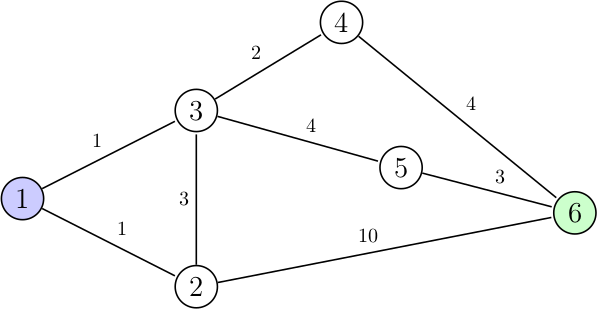
Soit le graphe suivant :

On souhaite trouver le plus court chemin pour aller du nœud de départ (en bleu) au nœud d'arrivée (en vert).
L'algorithme de Dijkstra commence par le nœud de départ (1), et examine ses voisins :

Le nœud en bleu représente désormais le nœud en tête de notre file à priorité, et j'ai aussi indiqué la distance parcourue depuis le nœud initial en indice. Le nœud 1 possède deux arcs qui représentent donc deux possibilités pour le moment. L'algorithme prend en compte la distance depuis le nœud de départ ainsi que le poids des arcs pour choisir le prochain nœud à visiter. Les différentes combinaisons actuellement sont donc : 0 + 1 (nœud 1 vers nœud 2) et 0 + 1 (1 vers 3). Dans notre cas les deux nœuds sont équivalents en termes d'efficacité, mais notre implémentation doit bien choisir lequel parcourir et nous imaginerons que l'on visite le nœud 2 (le nœud 3 menant directement au plus court chemin, il est plus intéressant de voir comment notre algorithme va rectifier son tir). Notre file à priorité contient donc les nœuds 2 et 3 (le 1 a été retiré), mais le 2 apparait avant c'est donc celui-ci qu'on va visiter au prochain tour :
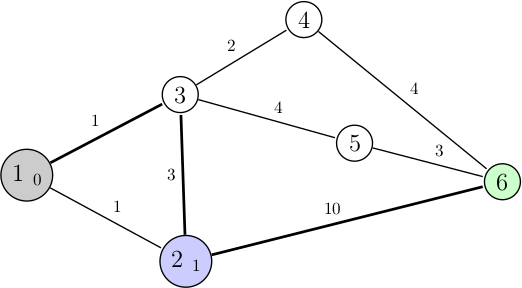
Notre algorithme nous mène au nœud 2, avec comme distance totale 1. Le point très important ici, est que lors du dernier tour, on avait deux choix possibles d'arcs à emprunter, en choisissant l'un des deux on n'oublie pas de conserver l'autre au cas où justement ce n'est pas le chemin le plus optimal qu'on vient de prendre. Et la file à priorité est le point essentiel car cette structure se chargera de faire remonter automatiquement le nœud 3 en tête si ce dernier devient finalement un choix plus intéressant. Lorsqu'on ajoute les voisins du nœud 2 à notre file, on doit choisir entre : 0 + 1 (nœud 1 vers 3), 1 + 3 (2 vers 3), ou 1 + 10 (2 vers 6). On voit que le minimum est atteint pour 0 + 1, soit le nœud 1 vers le 3. Notre file à priorité ne possède donc plus le nœud 2, et a en tête le nœud 3 qu'on parcourt lors du prochain tour :
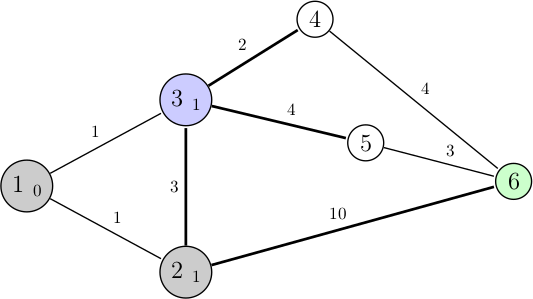
Nous sommes au nœud 3 avec une distance totale depuis le nœud de départ de 1, comme d'habitude on va chercher à comparer nos anciennes possibilités à celles qui se sont rajoutées (les voisins de 3). L'algorithme doit donc choisir entre : 1 + 2 (nœud 3 vers 4), 1 + 4 (3 vers 5), 1 + 3 (2 vers 3), et 1 + 10 (2 vers 6). Le choix avec une distance minimale est donc le premier : allant du nœud 3 vers le nœud 4. On continue l'algorithme :
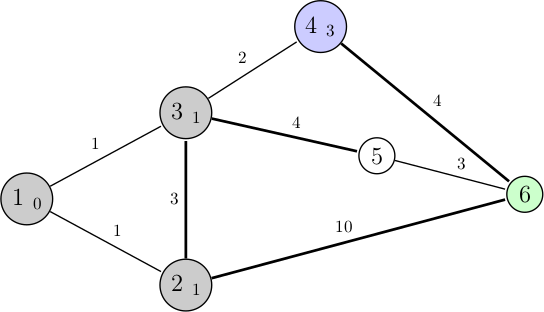
On se retrouve avec un nouvel arc disponible, et on va comparer de nouveau les différents chemins possibles : 3 + 4 (nœud 4 vers 6), 1 + 4 (3 vers 5), 1 + 3 (2 vers 3), et 1 + 10 (2 vers 6). L'algorithme choisit donc le chemin 2 vers 3 :

Cependant lorsqu'on arrive sur le nœud 3, on s'aperçoit qu'on a déjà visité ce nœud (il est donc tout à fait inutile de recommencer cette opération), et l'algorithme va immédiatement choisir un autre chemin entre : 3 + 4 (nœud 4 vers 6), 1 + 4 (3 vers 5), et 1 + 10 (2 vers 6). Le chemin choisi est donc celui reliant le nœud 3 au 5 :
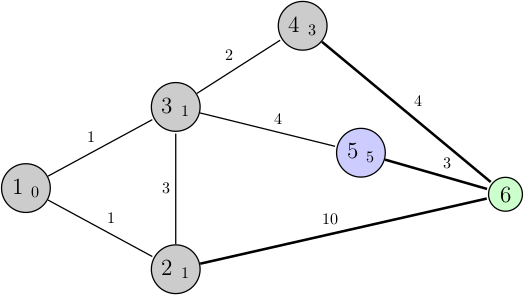
Comme auparavant, on prend en compte le nouvel arc possible et on choisit entre : 3 + 4 (nœud 4 vers 6), 5 + 3 (5 vers 6) et 1 + 10 (2 vers 6). Le premier choix étant celui avec le plus petit résultat, c'est ce qu'on décide de réaliser :
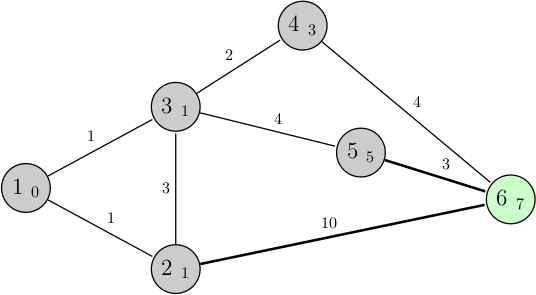
On arrive au nœud vert (celui d'arrivée), notre algorithme a donc terminé et on a trouvé le plus court chemin pour s'y rendre (les autres possibilités restantes étant forcément des chemins avec une plus longue distance).
Cet exemple peut prêter à confusion car finalement on a visité tous les nœuds du graphe ainsi que la plupart des arcs, mais j'ai choisi ceci pour justement montrer au mieux le fonctionnement de l'algorithme et surtout comment ce dernier réalise son choix pour trouver le chemin optimal en termes de distance. Sur d'énormes graphes, l'algorithme de Dijkstra est très utile car il ne visitera que ce dont il a réellement besoin puisque si on réfléchit à sa manière de fonctionner, on ne peut pas savoir à l'avance si le chemin qu'il emprunte actuellement restera optimal jusqu'au bout (d'où la nécessité de conserver les différents choix rencontrés lors du parcours), et inversement il se peut que les autres chemins soient en réalité pires et qu'il faut donc bien garder celui actuel.
Le pseudo-code de l'algorithme de Dijkstra est donc identique à celui du parcours en profondeur, sauf qu'on utilise une file à priorité au lieu d'une file, afin d'organiser les éléments en fonction de leur distance au nœud de départ :
Dijkstra (départ, arrivée) :
départ.distance = 0
Enfiler le nœud de départ
Tant que la file à priorité n'est pas vide
Défiler le nœud au début de la file
Si c'est le nœud d'arrivée
Retourner nœud.distance
Marquer le nœud comme visité
Pour chaque voisin du nœud
Si le voisin n'est pas visité
voisin.distance = nœud.distance + arc
Enfiler le voisinLa complexité de cet algorithme peut énormément changer en fonction de son implémentation, et il est important de comprendre pourquoi mais surtout comment.
On sait que notre file à priorité nous permet deux opérations d'insertion et de suppression en un temps logarithmique de \(O(\log _2 x)\) avec \(x\) le nombre d'éléments de la file. Dans notre cas, un nœud peut être ajouté à notre file autant de fois qu'il y a d'arcs qui le précédent, ce qui signifie que dans le pire des cas on aura \(M\) éléments dans la file à priorité. De même, dans le pire des cas, on devra supprimer ces \(M\) éléments de la file (si le dernier élément est celui qu'on cherche), résultant en \(M\) insertions et \(M\) suppressions au maximum. Notre complexité en temps est donc de \(O(M \log _2 M + M \log _2 M)\) soit \(O(2M \log _2 M)\) qu'on peut simplifier en \(O(M \log _2 M)\) car 2 est une constante insignifiante pour des valeurs de \(M\) élevées.
Cependant, il est possible d'améliorer le nombre d'éléments dans notre file à priorité en mettant à jour les valeurs des nœuds déjà enfilés, plutôt que de recréer des éléments en plus dans la file. Cette opération s'effectue aussi en temps logarithmique, et nous permet de garder au maximum \(N\) éléments dans notre file. Finalement, on a donc dans le pire des cas \(N\) insertions, \(N\) suppressions, et \(M\) mises à jour d'éléments dans la file. Ceci nous donne une nouvelle complexité en temps de \(O(2N \log _2 N + M \log _2 N)\) que l'on peut simplifier en \(O(M \log _2 N)\) car dans la plupart des cas on aura \(M \geq N\).
Enfin, on peut encore améliorer notre complexité en temps si l'on utilise une variante de la file à priorité : le tas de Fibonacci. Cette structure a un temps constant pour l'insertion et la mise à jour d'éléments, ce qui nous donne une complexité finale de \(O(N + N \log _2 N + M)\), et si l'on suppose que de manière générale on a \(M \geq N\), on peut écrire cette complexité en temps comme ceci : \(O(N \log _2 N + M)\).
Une implémentation en C++ (pour avoir priority_queue) de cet algorithme (sans les améliorations de complexité proposées dans la dernière partie) :
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
struct Noeud
{
int index;
int distance;
bool operator < (const Noeud &autre) const
{
if(distance < autre.distance)
return false;
else
return true;
}
};
const int NB_NOEUD_MAX = 1000;
vector <Noeud> voisin[NB_NOEUD_MAX];
bool dejaVu[NB_NOEUD_MAX];
int dijkstra(int depart, int arrivee)
{
priority_queue <Noeud> file;
Noeud initial, actuel;
int iVoisin;
initial.index = depart;
initial.distance = 0;
file.push(initial);
while(!file.empty()) {
actuel = file.top();
file.pop();
if(actuel.index == arrivee)
return actuel.distance;
if(dejaVu[actuel.index])
continue;
dejaVu[actuel.index] = true;
for(iVoisin = 0; iVoisin < voisin[actuel.index].size(); ++iVoisin) {
if(!dejaVu[voisin[actuel.index][iVoisin].index]) {
Noeud nouveau;
nouveau.index = voisin[actuel.index][iVoisin].index;
nouveau.distance = actuel.distance +
voisin[actuel.index][iVoisin].distance;
file.push(nouveau);
}
}
}
return -1;
}
int main(void)
{
int depart, arrivee;
int nbArc;
int iArc;
scanf("%d %d\n", &depart, &arrivee);
scanf("%d\n", &nbArc);
for(iArc = 0; iArc < nbArc; ++iArc) {
int noeud1, noeud2, distance;
Noeud nouveau;
scanf("%d %d %d\n", &noeud1, &noeud2, &distance);
nouveau.distance = distance;
nouveau.index = noeud2;
voisin[noeud1].push_back(nouveau);
nouveau.index = noeud1;
voisin[noeud2].push_back(nouveau);
}
printf("%d\n", dijkstra(depart, arrivee));
return 0;
}La structure du code est identique à celle du parcours en profondeur,
on doit juste utiliser une structure afin de représenter nos nœuds (du
graphe, et de notre file) et aussi décrire l'opérateur <
pour que l'implémentation de la priority_queue puisse
fonctionner correctement en fonction de la variable
distance de chacun des nœuds.
En entrée, pour décrire notre graphe on va d'abord indiquer le nœud
de départ et d'arrivée, puis le nombre d'arcs et enfin la liste de ces
derniers du style nœud1 nœud2 poids (qu'on appelle aussi liste d'arcs):
1 6
8
1 2 1
1 3 1
2 3 3
2 6 10
3 4 2
3 5 4
4 6 4
5 6 3Et le plus court chemin en sortie :
7J'ai précisé au début de mes explications que l'algorithme de Dijkstra ne s'appliquait que sur des graphes pondérés positivement (ou nul), mais pourquoi ? Voici tout d'abord un contre-exemple pour prouver cette propriété :
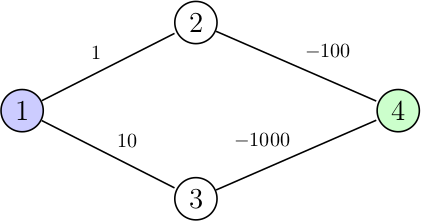
Regardons ce qui se passe si on utilise notre algorithme pour trouver le plus court chemin entre le nœud 1 et 4 :
| Tour | Nœud actuel | Distance totale | Choix |
|---|---|---|---|
| 1 | 1 | 0 | 0 + 1 (1 vers 2) ou 0 + 10 (1 vers 3) |
| 2 | 2 | 1 | 1 - 100 (2 vers 4) ou 0 + 10 (1 vers 3) |
| 3 | 4 | -99 |
On voit bien que le chemin trouvé a une distance totale de -99, cependant on peut faire mieux en empruntant le chemin suivant : 1, 3, 4 pour une distance de -990. L'algorithme ne voit pas le nœud 3 comme intéressant car l'arc permettant d'y accéder a un poids de 10 alors que sur le chemin actuel notre poids est bien inférieur à ce dernier, du coup on n'atteindra jamais l'arc de -1000 séparant le nœud 3 et 4 qui offre un chemin optimal jusqu'à l'arrivée.
L'algorithme de Dijkstra ne fonctionne donc pas sur ce genre de graphe, et ceci pour une simple raison : c'est un algorithme dit glouton. Cela signifie qu'il va chercher à faire des choix locaux optimaux (c'est-à-dire à un instant t bien précis), pour espérer trouver un choix global optimal aussi. Dans notre cas, on cherche à emprunter à un instant t le chemin avec le poids le plus faible possible (tout en considérant la distance déjà parcourue), pour espérer tomber sur le nœud d'arrivée avec une distance minimale (ce qui est démontrable). L'algorithme se base donc sur le fait que rajouter un arc ne peut jamais améliorer le chemin (puisque les poids sont forcément positifs ou nuls), et il ne peut donc pas fonctionner avec des poids négatifs (qui eux peuvent dans certains cas améliorer le coût total).
On pourrait penser qu'une solution face à ce problème serait de rajouter à tous les arcs un certain poids afin de les rendre positifs, mais encore une fois cette idée ne fonctionne pas :
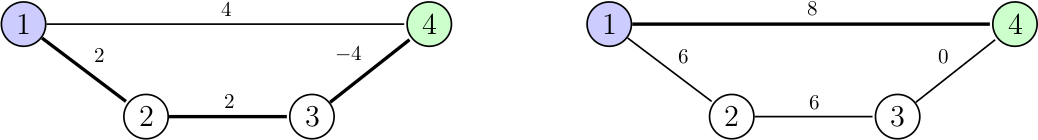
À gauche un graphe avec des pondérations négatives, et à droite l'équivalent mais cette fois on a rajouté 4 à chaque poids pour n'avoir que des arcs positifs ou nuls. On veut dans les deux cas trouver le plus court chemin entre les nœuds 1 et 4 et on voit clairement que dans notre graphe original, le chemin optimal est 1, 2, 3, 4, mais dans notre nouveau graphe avec le changement de pondération, le chemin 1, 4 est plus optimal. Il n'est donc pas possible d'utiliser l'algorithme de Dijkstra sur un graphe qui n'a pas naturellement de pondérations positives ou nulles.
L'algorithme de Dijkstra est donc un algorithme glouton de recherche de plus court chemin dans un graphe pondéré positivement, avec une complexité en temps intéressante de \(O(M \log _2 M)\) (pouvant cependant être améliorée en \(O(N \log _2 N + M)\)). L'algorithme en lui-même pose principalement deux problèmes :