Le parcours d'un graphe est une opération essentielle à connaître à propos de cette structure. Il est fondamental de maitriser les différents algorithmes de parcours de graphe, ainsi que leur application et surtout savoir quand les utiliser en fonction de la situation.
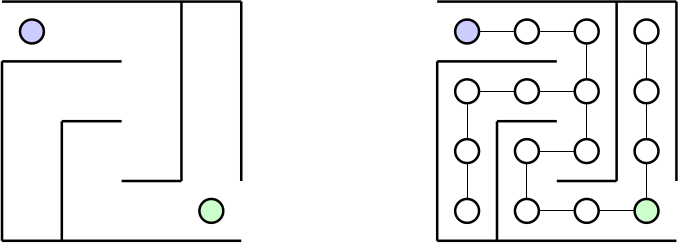
Vous vous trouvez dans un labyrinthe contenant de nombreux chemins possibles, et vous cherchez la sortie alors que vous ne connaissez aucunes indications sur ce labyrinthe. Tout d'abord, on peut représenter notre labyrinthe comme un graphe dit implicite, qui sera non pondéré (chaque arc aura alors une distance de 1 unité). En effet, chaque intersection sera représentée par un nœud du graphe, et chaque chemin par un arc. L'entrée et la sortie du labyrinthe sont juste de simples nœuds distincts du graphe, et le fait de trouver la sortie du labyrinthe, revient à trouver un chemin reliant le nœud d'entrée au nœud de sortie :

Vu qu'on ne connait rien sur ce labyrinthe, il est impossible de deviner le chemin nous permettant d'arriver à la sortie puisque ça pourrait être n'importe lequel du graphe. On peut donc tout simplement essayer chacun des chemins jusqu'à trouver le bon. Ce parcours est alors qualifié de : parcours en profondeur.
Le parcours en profondeur (ou plus communément DFS pour Depth First Search) permet de parcourir un graphe en utilisant le principe de la récursivité. Ce parcours visite les nœuds du graphe les plus "profonds" en premier (c'est-à-dire les plus éloignés du nœud de départ), avant de "remonter" progressivement dans le graphe.
Dans notre cas du labyrinthe, on essaie un chemin jusqu'à être bloqué, puis on revient à la dernière intersection, on continue jusqu'à être bloqué, on revient à la dernière intersection, etc. jusqu'à tomber sur la sortie.
La meilleure manière de comprendre ce type de parcours est de le visualiser :
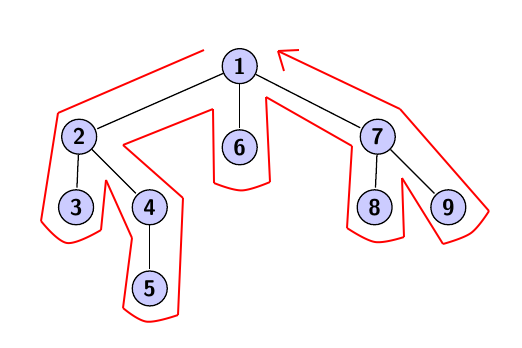
Ce graphe représente notre labyrinthe, et chaque nœud correspond à l'ordre de parcours du DFS (la flèche montre uniquement comment agit un parcours en profondeur en entier sur notre graphe).
Si par exemple notre entrée de labyrinthe est le nœud 1, et que notre sortie est le nœud 6, on parcourra avant de trouver la sortie, les nœuds 2, 3, 4, et 5.
Cependant sur un graphe, on peut effectuer un DFS de différentes façons en fonction de l'ordre de visite des voisins. Par exemple, on aurait pu après le nœud 1 visiter le nœud 7, puis le 9, puis le 8, puis le 6, le 2, le 4, le 5, et enfin le 3. Ce parcours est bien un DFS, mais il est juste différent car on a choisi un autre ordre pour parcourir les voisins des nœuds rencontrés.
On utilise le principe de la récursivité pour définir notre parcours en profondeur :
DFS (nœud) :
Marquer le nœud comme visité
Pour chaque voisin du nœud passé en paramètre
Si le voisin n'est pas marqué visité
DFS(voisin)Si par exemple on cherche un nœud de sortie dans notre graphe, on pourrait rajouter une condition qui arrêtera le DFS lorsqu'on a visité ce nœud. Cependant ici, le DFS parcourt tout le graphe à titre d'exemple.
Dans le pire des cas, si notre sortie est le dernier nœud que l'on visite, notre algorithme va devoir parcourir les \(M\) arcs du graphe, on a donc une complexité en temps linéaire de \(O(M)\).
On peut implémenter un DFS de deux manières différentes, même si on a plutôt tendance à le coder de manière récursive car le code est plus court et plus intuitif.
Une implémentation récursive en C++ (j'utilise le C++ afin d'avoir
les vector pour représenter notre graphe) :
#include <cstdio>
#include <vector>
using namespace std;
const int NB_NOEUD_MAX = 1000;
vector <int> graphe[NB_NOEUD_MAX];
bool dejaVu[NB_NOEUD_MAX];
void DFS(int noeud)
{
printf("%d\n", noeud);
dejaVu[noeud] = true;
int iVoisin;
for(iVoisin = 0; iVoisin < graphe[noeud].size(); ++iVoisin)
if(!dejaVu[graphe[noeud][iVoisin]])
DFS(graphe[noeud][iVoisin]);
}
int main(void)
{
int nbArc;
int iArc;
scanf("%d\n", &nbArc);
for(iArc = 0; iArc < nbArc; ++iArc) {
int noeud1, noeud2;
scanf("%d %d\n", &noeud1, &noeud2);
graphe[noeud1].push_back(noeud2);
}
DFS(1);
return 0;
}Si en entrée on donne notre graphe (celui de l'exemple et sous forme d'une liste d'arcs) :
8
1 2
1 6
1 7
2 3
2 4
4 5
7 8
7 9On obtient bien en sortie :
1 2 3 4 5 6 7 8 9Et pour vous montrer que l'ordre d'un parcours en profondeur peut changer selon l'ordre des voisins visités, prenons le même graphe mais avec un ordre différent dans sa description (l'ordre inverse) :
8
1 7
1 6
1 2
7 9
7 8
2 4
2 3
4 5En sortie cette fois on a :
1 7 9 8 6 2 4 5 3Il est rare d'implémenter de façon itérative un parcours en profondeur, mais cela peut être utile pour ne pas faire exploser la pile d'appels à cause des nombreux appels récursifs imbriqués provoqués par notre dernière implémentation.
Pour passer de la version récursive à la version itérative, on utilise simplement une pile afin de "simuler" la pile d'appel. En effet lorsqu'on visite un nœud, on veut visiter tout de suite ses voisins, il faut donc les placer dans l'ordre de visite avant les autres nœuds, on va donc les empiler afin de les parcourir d'abord.
#include <cstdio>
#include <vector>
#include <stack>
using namespace std;
const int NB_NOEUD_MAX = 1000;
vector <int> graphe[NB_NOEUD_MAX];
bool dejaVu[NB_NOEUD_MAX];
void DFS(int debut)
{
stack <int> pile;
int actuel;
int iVoisin;
pile.push(debut);
while(!pile.empty()) {
actuel = pile.top();
pile.pop();
printf("%d\n", actuel);
dejaVu[actuel] = true;
for(iVoisin = 0; iVoisin < graphe[actuel].size(); ++iVoisin)
if(!dejaVu[graphe[actuel][iVoisin]])
pile.push(graphe[actuel][iVoisin]);
}
}
int main(void)
{
int nbArc;
int iArc;
scanf("%d\n", &nbArc);
for(iArc = 0; iArc < nbArc; ++iArc) {
int noeud1, noeud2;
scanf("%d %d\n", &noeud1, &noeud2);
graphe[noeud1].push_back(noeud2);
}
DFS(1);
return 0;
}En entrée :
8
1 2
1 6
1 7
2 3
2 4
4 5
7 8
7 9Et la sortie affichée :
1 7 9 8 6 2 4 5 3Et si on donne notre entrée modifiée (à l'envers) :
8
1 7
1 6
1 2
7 9
7 8
2 4
2 3
4 5On a en sortie cette fois :
1 2 3 4 5 6 7 8 9Vous constatez donc que la pile "inverse" l'ordre, tout simplement car lorsqu'on parcourt la liste des voisins, on ne visite pas le voisin dès qu'on en a trouvé un non visité (comme le fait la version récursive), mais on les empile tous, et ils vont donc se superposer (ce qui va "inverser" l'ordre car c'est le principe d'une pile : le dernier arrivé, le premier sorti).
Vous vous retrouvez face à l'entrée du labyrinthe, mais cette fois ci vous cherchez le nombre de pas minimum que vous devez faire pour atteindre la sortie. Ce problème peut être vu comme un plus court chemin, mais notre graphe implicite est non pondéré contrairement aux autres algorithmes "classiques" de plus court chemin où le graphe est pondéré (positivement ou négativement). Cela revient donc à trouver un chemin entre l'entrée et la sortie comportant un minimum de nœuds possible (vu que les arcs ont chacun une distance de 1 unité). Mais de nouveau nous n'avons aucunes informations sur le labyrinthe, et la sortie pourrait se trouver n'importe où.
Essayons tout d'abord de voir si on peut réutiliser un algorithme de parcours en profondeur pour résoudre notre problème :
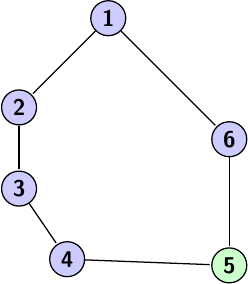
Dans cet exemple, on fait un DFS sur notre graphe et à cause de l'ordre de parcours des voisins on arrive à la sortie (le nœud vert) en passant par les nœuds 2, 3 et 4 alors qu'on peut y accéder en passant uniquement par le nœud 6. Bien sûr notre DFS aurait pu passer par le nœud 6 en premier et ainsi atteindre la sortie le plus rapidement possible, mais cet exemple montre l'un des problèmes du DFS pour ce genre d'exercice, c'est que le résultat de l'algorithme dépend de l'ordre de parcours des voisins qui peut totalement changer en fonction de l'implémentation mais aussi en fonction du graphe. Il nous faut donc un algorithme de parcours qui ne dépend d'aucuns de ces facteurs, et qui nous permet de trouver le chemin le plus court sur un graphe non pondéré : le parcours en largeur.
Le parcours en largeur (ou BFS pour Breadth First Search), visite les nœuds du graphe par ordre de profondeur. C'est-à-dire que l'algorithme va d'abord visiter les nœuds à une profondeur de 1 par rapport au nœud de départ, puis à une profondeur de 2, de 3, etc. On parcourt le graphe "couche par couche" contrairement au parcours en profondeur qui lui va chercher à aller le plus loin possible d'abord pour ensuite remonter.
Cela permet donc de trouver le plus court chemin sur un graphe non pondéré, car l'algorithme va regarder si on peut atteindre la sortie en parcourant un nœud de distance par rapport à l'entrée, puis deux nœuds, puis trois, etc. jusqu'à trouver la sortie. Finalement, on est sûr d'avoir trouvé le plus court chemin car il n'y a pas d'autres chemins comportant moins de nœuds pour accéder à la sortie.
Avec le même graphe que pour le DFS, mais en appliquant un BFS dessus :
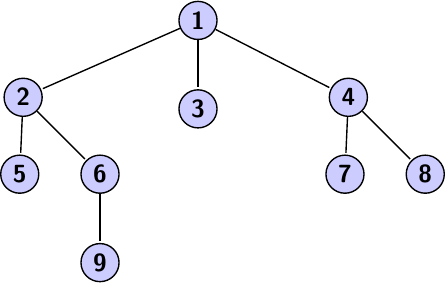
De même, chaque nœud représente l'ordre de parcours dans le graphe, et on retrouve bien cette idée de parcours par couche.
Pour implémenter ce système de parcours par niveau, on va utiliser une file. En effet, quand on est sur une couche \(N\), on veut que les voisins qu'on va parcourir lors de la couche \(N + 1\) soient tous situés après les nœuds de la couche \(N\) que l'on visite actuellement, on veut donc qu'ils arrivent à la fin et ce principe respecte l'ordre du premier entré, premier sorti qu'on appelle aussi une file.
BFS (depart) :
Enfiler le nœud de départ
Tant que la file n'est pas vide
Défiler le nœud au début de la file
Marquer le nœud comme visité
Pour chaque voisin du nœud
Si le voisin n'est pas visité
Enfiler le voisinComme pour le parcours en profondeur, si notre sortie est le dernier nœud que l'on visite on aura une complexité en \(O(M)\) avec \(M\) le nombre d'arcs du graphe.
L'implémentation du parcours en largeur en C++ (afin d'avoir le type
queue et vector) :
#include <cstdio>
#include <vector>
#include <queue>
using namespace std;
const int NB_NOEUD_MAX = 1000;
vector <int> graphe[NB_NOEUD_MAX];
bool dejaVu[NB_NOEUD_MAX];
void BFS(int debut)
{
queue <int> file;
int actuel;
int iVoisin;
file.push(debut);
while(!file.empty()) {
actuel = file.front();
file.pop();
printf("%d\n", actuel);
dejaVu[actuel] = true;
for(iVoisin = 0; iVoisin < graphe[actuel].size(); ++iVoisin)
if(!dejaVu[graphe[actuel][iVoisin]])
file.push(graphe[actuel][iVoisin]);
}
}
int main(void)
{
int nbArc;
int iArc;
scanf("%d\n", &nbArc);
for(iArc = 0; iArc < nbArc; ++iArc) {
int noeud1, noeud2;
scanf("%d %d\n", &noeud1, &noeud2);
graphe[noeud1].push_back(noeud2);
}
BFS(1);
return 0;
}Notre graphe :
8
1 2
1 3
1 4
2 5
2 6
4 7
4 8
6 9La sortie :
1 2 3 4 5 6 7 8 9Savoir parcourir un graphe est fondamental pour utiliser d'autres algorithmes de graphe plus complexes, et il existe deux types de parcours qu'il faut connaître et maitriser pour les utiliser au bon moment :
Toutes ces applications des deux algorithmes ne sont que des exemples, et le parcours choisi dépendra énormément du graphe en entrée. Il faut toujours réfléchir au problème donné avant d'utiliser un parcours (par exemple si on cherche un nœud précis et que ce dernier se situe proche du nœud de départ, un DFS sera un mauvais choix face au BFS). Il n'y a pas de manière de savoir quand utiliser l'un pas rapport à l'autre, à part en pratiquant le plus possible les deux types de parcours pour maitriser les avantages/désavantages et leurs utilisations.