Supposons que je souhaite faire le tour de l'Europe en passant par diverses villes de plusieurs pays. Comment représenter mon trajet ? Comment rajouter des contraintes supplémentaires si par exemple je désire faire un trajet défini, mais le plus court possible en termes de km ? Comment insérer ou supprimer une nouvelle destination dans mon voyage et surtout comment visualiser ce dernier ?
Naturellement, on pourrait prendre une carte et tracer des traits entre chaque ville de l'itinéraire afin de pouvoir le représenter, mais comment le faire comprendre à un ordinateur pour qu'il puisse le manipuler ? Nous avons donc besoin d'une structure de données flexible, permettant de visualiser des chemins entre différents points : le graphe.
On peut définir un graphe comme étant un ensemble de nœuds (ou de sommets) étant reliés par des arcs (ou des arêtes, des chemins).

En anglais, on parle de nodes ou vertices pour les nœuds, et d'*edges* ou arcs pour les arêtes.
Pour information, si deux nœuds sont reliés par un arc on dit qu'ils sont voisins. De plus, le degré entrant d'un nœud correspond au nombre d'arcs arrivant sur ce nœud, et il en est de même pour le degré sortant correspondant alors au nombre d'arcs sortant du nœud.
Un graphe peut avoir de nombreuses caractéristiques différentes, en voici une liste que l'on retrouve couramment :
| Caractéristique | Description | Exemple |
|---|---|---|
| Orienté | Si les arcs ont un sens (représenté par une flèche), le graphe est orienté. | 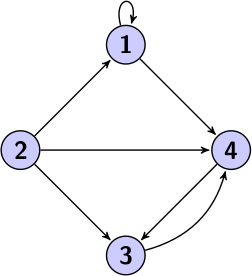 |
| Non orienté | Dans ce cas, on peut parcourir le graphe dans les deux sens. | 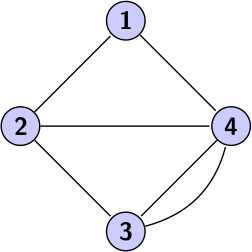 |
| Pondéré / non pondéré | Un graphe est pondéré si ses arcs ont un poids (par exemple la distance en km entre deux villes). | 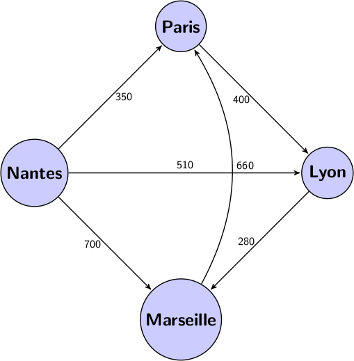 |
| Cyclique | Un graphe est cyclique s'il contient des chemins finissant là où ils ont commencé (des cycles). | 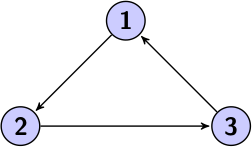 |
| Acyclique | Lorsque le graphe ne contient aucun cycle, il est acyclique. | 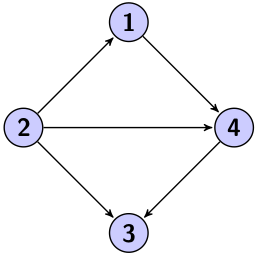 |
| Dense | Si le nombre d'arcs est proche du nombre maximum d'arcs possibles de ce graphe, il est dense. | 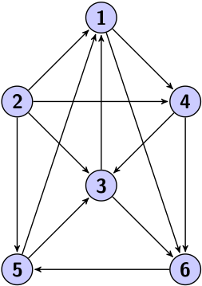 |
| Creux | Au contraire, si le nombre d'arcs est faible par rapport au nombre de nœuds, il est caractérisé de creux. | 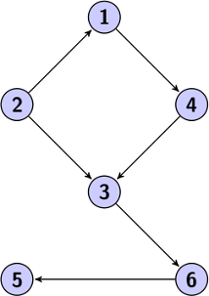 |
| Connexe / non connexe | Un graphe est dit connexe s'il existe un chemin (de un ou plusieurs nœuds) reliant chaque paire de nœuds possible. | 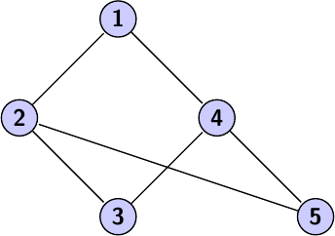 |
On peut implémenter un graphe de différentes façons, en fonction de nos besoins mais aussi de nos capacités (en temps et en mémoire).
Une matrice d'adjacence est comme son nom l'indique un tableau 2D qui
permet de représenter des arcs entre deux nœuds. On peut utiliser un
tableau 2D de booléen (true = arc, false = pas
d'arc), ou bien un tableau 2D d'entier (ou de flottant) qui permet alors
de stocker les pondérations des arcs (\(x\) = pondération de l'arc, 0 = pas
d'arc).
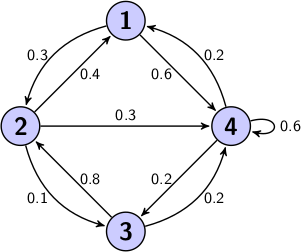
Voici un exemple de matrice d'adjacence (j'ai utilisé le premier graphe de l'article pour construire la matrice) :


Rien de bien compliqué pour l'implémenter :
int graphe[NB_NOEUD_MAX][NB_NOEUD_MAX];Encore une fois, on peut changer le type de la matrice en fonction de
nos besoins (bool, float, double,
etc.).
On utilise ce type de représentation lorsqu'on a tout d'abord assez de mémoire, puis lorsqu'on a besoin d'accéder souvent et rapidement à des informations du type :
La complexité en mémoire est en \(O(N^2)\) (avec \(N\) le nombre de nœuds du graphe), et la complexité pour accéder aux deux informations citées au-dessus est en \(O(1)\) (puisqu'il s'agit d'un tableau).
On peut utiliser une variante de la matrice d'adjacence afin d'économiser de la mémoire (mais cette représentation requiert un temps en \(O(N)\) pour savoir si deux nœuds sont voisins ou pour connaître la pondération d'un arc). Cette solution consiste à utiliser un tableau de listes chaînées, chaque nœud du graphe a sa propre liste chaînée contenant tous ses voisins (et éventuellement toutes les pondérations).
Voici par exemple la liste d'adjacence qui représente de nouveau le premier graphe de l'article :

Pour l'implémentation, j'utilise les vector du C++ au lieu de recoder à la main la liste chaînée en C (même si on peut tout à fait le faire, recoder des structures de données basiques peut être une perte de temps, notamment pendant un concours de programmation) :
vector <Voisin> graphe[NB_NOEUD_MAX];La structure Voisin contient l'index du voisin, mais
elle peut aussi contenir la pondération de l'arc liant les deux nœuds,
voir d'autres informations spécifiques au graphe.
La liste d'adjacence est le plus souvent utilisée lorsque :
Enfin on peut utiliser une dernière solution, en représentant tous les arcs du graphe dans une liste chaînée.
Voici l'exemple d'une liste d'arcs (toujours sur le même graphe) :
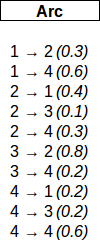
De même que pour la liste d'adjacence, j'utilise les
vector :
vector <Arc> graphe;La structure Arc contient l'index des deux nœuds ainsi
que la pondération de l'arc (si c'est un graphe pondéré).
Une liste d'arcs est plus rarement utilisée pour représenter un graphe, mais peut s'avérer très utile lorsqu'on n'a pas assez de mémoire (à cause du nombre trop élevé de nœuds) pour représenter le graphe avec une matrice d'adjacence ou même une liste d'adjacence. On utilise donc une liste d'arcs avec une complexité en mémoire de \(O(M)\).
Afin de parcourir notre graphe, on peut utiliser deux algorithmes différents :
Voici une liste non exhaustive d'opérations utiles lorsqu'on manipule un graphe :
Un graphe est une structure de données incontournable, utilisée dans de très nombreux problèmes (plus ou moins complexes) de la vie de tous les jours et dans beaucoup de domaines différents comme :