L'approche gloutonne de l'algorithme de Dijkstra est excellente car elle permet d'aborder le problème du plus court chemin de manière intelligente, ce qui lui donne une complexité en temps intéressante, tout en étant optimale. Cependant, elle ne s'applique pas à toutes les configurations de graphes (par exemple ceux avec des pondérations négatives), et il nous faut donc un nouvel algorithme pour gérer ces cas.
Reprenons depuis le début. On a un graphe pondéré (positivement ou négativement), et on cherche le plus court chemin entre deux nœuds distincts. Une approche naïve serait d'explorer toutes les combinaisons possibles de chemin et de choisir celle qui obtient une pondération totale minimale. Le problème ici est évidemment la complexité en temps exponentielle. Dans ce genre de situation, il est fondamental de se poser cette question : qu'est-ce qui rend notre algorithme si lent ? Lorsqu'on explore toutes les possibilités de chemins, on repasse très souvent sur d'anciens nœuds et arcs, ce qui nous fait parcourir notre graphe plusieurs fois inutilement.
Désormais, on connaît la raison de la lenteur de notre précédent algorithme, et il faut alors chercher à améliorer ce point, si possible, ou bien à changer de concept. L'algorithme de Bellman-Ford va améliorer l'algorithme naïf, en utilisant une approche différente du problème : la programmation dynamique. L'idée est justement de ne pas repasser plusieurs fois sur des parties du graphe, mais plutôt de garder les informations utiles en mémoire à l'aide d'un algorithme dynamique, et de les réutiliser intelligemment.
Il est intéressant de noter que `Richard Bellman <https://en.wikipedia.org/wiki/Richard_E._Bellman>`__, l'un des inventeurs de cet algorithme, est le père fondateur de la programmation dynamique.
Un exemple de l'algorithme de Bellman-Ford serait assez peu intéressant car il n'adopte pas de stratégie particulière au niveau du parcours du graphe (contrairement à l'algorithme de Dijkstra). Il se contente uniquement de tester chaque possibilité de chemin avec une implémentation dynamique le rendant plus rapide qu'une implémentation naïve. Cependant, nous allons voir un exemple au travers du pseudo-code afin de comprendre son fonctionnement.
Pour appréhender au mieux cette partie, il est nécessaire d'être familier à la programmation dynamique (ou au moins d'en connaître la base). Si ce n'est pas le cas, je vous renvoie vers mon `article sur le sujet </algo/general/approche/dynamique.html>`__.
Pour mettre en place un algorithme dynamique correctement, il est essentiel de rédiger la version récursive d'abord afin d'établir explicitement la récursion pour bien comprendre ce que cherche à réaliser l'algorithme. Nous allons donc procéder par étape pour ce pseudo-code, en commençant par la version récursive naïve, puis nous l'améliorerons petit à petit grâce à un algorithme dynamique.
Avant de se plonger dans le pseudo-code, il faut noter que le problème du plus court chemin sur un graphe pondéré positivement et négativement introduit un nouveau souci : les cycles améliorants (ou negative cycle en anglais). En effet, vu qu'une pondération peut désormais être négative, il est possible de tomber dans une boucle infinie (qu'on appelle plus précisément un cycle améliorant) qui va sans cesse diminuer la distance parcourue. Ceci pose un réel problème puisqu'on peut améliorer la distance à chaque fois qu'on passe dans ce cycle, et il existera toujours un meilleur chemin à emprunter. Lorsqu'un graphe contient ce genre de cycle, il n'y a pas de solution à cause de cette boucle infinie, il faut donc pouvoir le détecter.

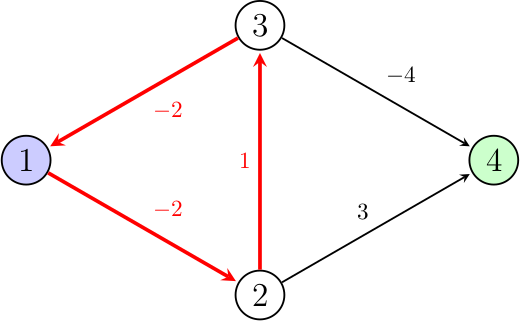
Sur cet exemple de graphe (avec le nœud de départ en bleu, et celui d'arrivée en vert), on remarque que le chemin surligné en rouge est un cycle améliorant. En effet, dès qu'on parcourt ce cycle, la distance parcourue en sortie sera toujours inférieure à celle en entrée, d'où l'intérêt de le visiter à nouveau afin de diminuer encore la distance, et ainsi de suite, ce qui entraine une boucle infinie. Il est impossible de trouver le plus court chemin entre le nœud 1 et 4 dans ce graphe, car on peut améliorer la distance parcourue à l'infini sans jamais arriver au nœud en vert.
Pour contrer cela, on va imposer une limite de recherche à notre récursion qui ne pourra pas dépasser l'exploration de \(K\) nœuds. Une limite de \(N\) nœuds maximum à explorer permet à notre algorithme de ne jamais tomber dans une boucle infinie (avec \(N\) le nombre de nœuds du graphe), puisqu'un plus court chemin, qui ne contient pas de cycle améliorant, ne passe jamais plus de deux fois par un même nœud. On peut désormais reformuler clairement notre problème de plus court chemin entre un nœud A et B, en un problème cherchant à minimiser la distance entre A et B en réalisant \(K\) étapes au maximum. La reformulation du problème est importante puisqu'elle nous donne une idée plus claire de l'approche naïve que l'on va réaliser dans un premier temps.
Voici un premier pseudo-code simplifié de la récursion (on suppose que le graphe en entrée est orienté et ne possède pas de cycles améliorantes pour établir une première idée de l'algorithme général).
Bellman-Ford (nbÉtape, nœud) :
Si nbÉtape = 0
Si c'est le nœud d'arrivée
Retourner 0
Sinon
Retourner INFINI car le chemin est invalide
cheminMin = Bellman-Ford(nbÉtape - 1, nœud)
Pour chaque voisin du nœud
cheminVoisin = pondérationArc + Bellman-Ford(nbÉtape - 1, voisin)
cheminMin = min(cheminMin, cheminVoisin)
Retourner cheminMinCe pseudo-code traduit une simple récursion permettant d'explorer
tous les chemins en moins de nbÉtape jusqu'à l'arrivée,
tout en sélectionnant le plus court d'entre eux. Pour cela, l'algorithme
utilise une simple boucle sur tous les voisins d'un nœud ainsi qu'une
variable cheminMin qu'on actualise pour toujours avoir le
chemin avec la pondération minimale entre tous les choix possibles.
Maintenant, on passe à l'étape de dynamisation de cet algorithme puisque ce dernier est terriblement lent et possède une complexité en temps exponentielle car il ne fait que répéter des appels récursifs inutilement. On va donc créer un tableau 2D stockant le plus court chemin pour tous les paramètres possibles de notre fonction, afin de ne jamais avoir à recalculer le résultat d'un même appel.
plusCourtChemin[NB_ÉTAPE_MAX][NB_NŒUD_MAX] (initialisé à -1)
Bellman-Ford (nbÉtape, nœud) :
Si nbÉtape = 0
Si c'est le nœud d'arrivée
Retourner 0
Sinon
Retourner INFINI car le chemin est invalide
Si plusCourtChemin[nbÉtape][nœud] != -1
Retourner plusCourtChemin[nbÉtape][nœud]
cheminMin = Bellman-Ford(nbÉtape - 1, nœud)
Pour chaque voisin du nœud
cheminVoisin = pondérationArc + Bellman-Ford(nbÉtape - 1, voisin)
cheminMin = min(cheminMin, cheminVoisin)
plusCourtChemin[nbÉtape][nœud] = cheminMin
Retourner cheminMinOn a seulement ajouté les trois points fondamentaux qu'on retrouve dans un processus de dynamisation d'un algorithme :
plusCourtChemin à -1
pour marquer toutes les valeurs comme non calculées.Une fois qu'on a réussi à obtenir une complexité en temps non exponentielle (puisque désormais on ne parcourt pas inutilement des parties du graphe), il est toujours intéressant de tenter de réduire notre complexité en mémoire si possible. Dans notre dernier pseudo-code, on a une complexité mémoire de l'ordre de \(O(KN)\), ce qui est équivalent à du \(O(N^2)\), car on choisit la limite \(K\), tel que \(K = N\) pour éviter les cycles améliorants. Cet ordre de grandeur est tout à fait correct en termes d'espace mémoire, surtout vu le gain de temps qu'on acquiert grâce au tableau, mais il peut être encore largement amélioré.
Le passage à la version itérative de l'algorithme dynamique est essentiel à cette réduction de l'espace mémoire utilisé :
Bellman-Ford :
plusCourtChemin[NB_ÉTAPE_MAX][NB_NŒUD_MAX] (initialisé à INFINI)
plusCourtChemin[0][arrivée] = 0
Pour chaque étape
Pour chaque nœud
cheminMin = plusCourtChemin[étape - 1][nœud]
Pour chaque voisin du nœud
cheminVoisin = pondérationArc + plusCourtChemin[étape - 1][voisin]
cheminMin = min(cheminMin, cheminVoisin)
plusCourtChemin[étape][nœud] = cheminMin
Retourner plusCourtChemin[nbÉtapeMax - 1][départ]Plusieurs points importants à comprendre dans cette version itérative de l'algorithme :
plusCourtChemin est initialisé à
INFINI car on n'a plus besoin de détecter le cas où l'on
retombe sur un appel de fonction déjà rencontré auparavant, puisque
désormais on utilise des boucles (passage de la version récursive à
itérative). On choisit donc la valeur INFINI pour noter
qu'on ne connaît pas de plus court chemin pour un nœud donné à une étape
précise.plusCourtChemin, et c'est
exactement ce que réalisait implicitement notre fonction récursive
puisqu'on retrouve la première boucle grâce au paramètre de la fonction
nbÉtape (que l'on diminuait à chaque fois de 1, et qui nous
permettait d'arrêter la récursion lorsqu'elle atteignait 0), et la
boucle sur les nœuds lors des appels récursifs sur les nœuds
voisins.plusCourtChemin.Avant de réaliser l'économie de mémoire, attardons-nous légèrement sur ce dernier pseudo-code afin de bien comprendre comment effectuer cette amélioration. Prenons l'exemple de ce graphe (ne contenant pas de cycle améliorant pour simplifier la chose), et appliquons notre nouveau pseudo-code itératif dessus pour bien l'appréhender :
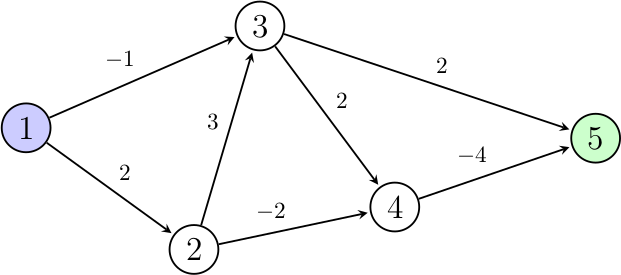
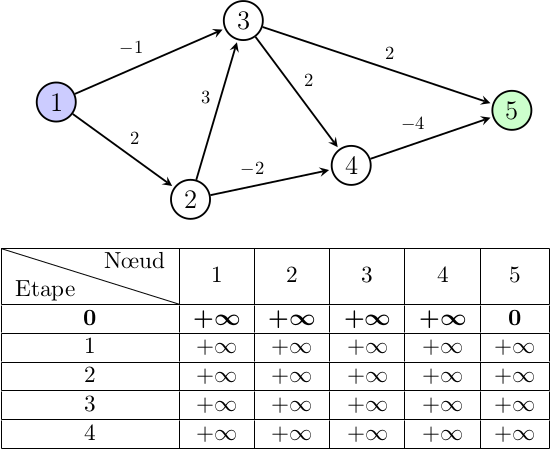
On cherche le plus court chemin entre le nœud 1 (en bleu) et le nœud
5 (en vert), et notre tableau plusCourtChemin initial
ressemble donc à cela :
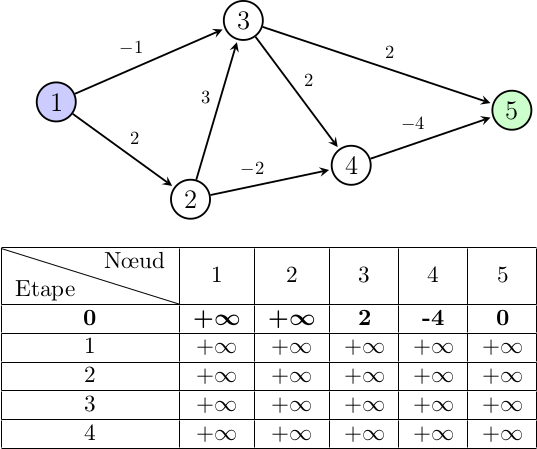
plusCourtCheminMaintenant qu'on a initialisé notre tableau, on peut commencer à le remplir. Pour rappel, chaque case de ce tableau représente la longueur du plus court chemin reliant un nœud au nœud d'arrivée :
La partie du pseudo-code nous concernant ici est la suivante :
Pour chaque étape
Pour chaque nœud
cheminMin = plusCourtChemin[étape - 1][nœud]
Pour chaque voisin du nœud
cheminVoisin = pondérationArc + plusCourtChemin[étape - 1][voisin]
cheminMin = min(cheminMin, cheminVoisin)
plusCourtChemin[étape][nœud] = cheminMinOn va donc décomposer l'explication de l'étape 0, afin de traiter séparément le cas de chaque nœud.
Pour le nœud 1, dans notre pseudo-code la ligne
cheminMin = plusCourtChemin[étape - 1][nœud] permet de
prendre en compte le dernier chemin trouvé pour un nœud, or ici c'est le
premier tour donc on n'a aucunes informations qu'on peut réutiliser. On
parcourt les voisins du nœud 1, soit les nœuds 2 et 3, et on calcule la
pondération du chemin reliant 1 au meilleur chemin qu'on a trouvé avec
ses voisins (cela correspond à la ligne
cheminVoisin = pondérationArc + plusCourtChemin[étape - 1][voisin]).
Encore une fois, on a aucunes informations sur des chemins pour aucun de
ses voisins, donc la case du nœud 1 reste inchangée dans notre
tableau.
De même, le nœud 2 se retrouve dans cette situation. En effet, on ne possède aucunes informations antérieures (puisque c'est l'étape 0), et aucun de ses voisins (nœuds 3 et 4) n'en possèdent non plus.
Le nœud 3 n'a aucunes précédentes informations, mais possède cependant comme voisin le nœud 5 (notre nœud d'arrivée). On peut donc trouver un chemin simple et direct entre le nœud 3 et 5, de pondération 2. Le nœud 4 est aussi voisin du nœud 3 mais ne possède encore aucunes données sur un éventuel chemin avec le nœud 5.
On arrive enfin au nœud 4 et lui aussi est relié directement à notre nœud d'arrivée, on peut donc mettre à jour sa case dans le tableau.
Finalement, le premier tour de boucle va uniquement calculer des chemins (on n'est pas encore sûr qu'ils sont les plus courts) des voisins directs du nœud d'arrivée, puisque les autres nœuds n'ont aucunes informations à ce sujet.
On recommence notre procédé sur les différents nœuds, mais cette fois on peut réutiliser les anciennes valeurs :
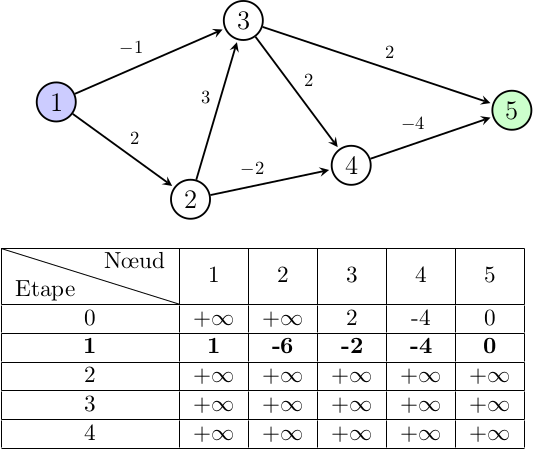
Pour le nœud 1, le seul de ses deux voisins à posséder des informations est le nœud 3. On a donc pas d'autres choix de chemin reliant le nœud 1 et 5 que celui-ci pour le moment.
Le nœud 2 en revanche peut utiliser les informations de ses deux voisins. On calcule donc le chemin qui minimise la pondération en choisissant le meilleur (ici, le chemin reliant 2, 3 et 5 a un coût total de 5 unités, et le chemin reliant 2, 4 et 5 a un coût de -6 unités, c'est donc ce dernier qu'on choisit).
Pour le nœud 3, on connaît maintenant des informations au sujet du nœud 4 et on peut alors les exploiter à notre avantage. En effet, emprunter le chemin reliant le nœud 4 et 5 nous avantage par rapport à un chemin direct entre 3 et 5.
Enfin le nœud 4 n'a pas d'autres voisins que le nœud 5 donc aucuns autres choix de chemin.
On continue comme ceci jusqu'à avoir rempli tout notre tableau :
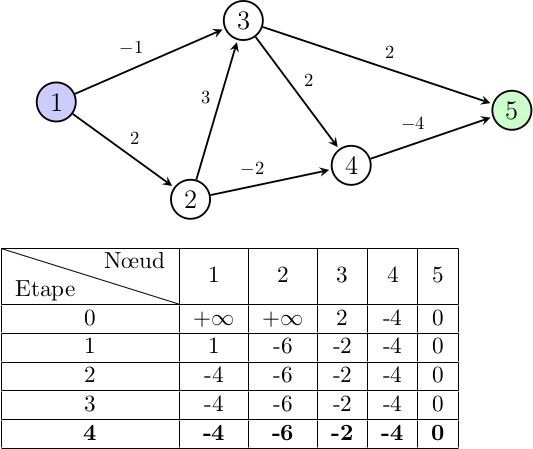
Désormais on connait le plus court chemin du graphe reliant le nœud 1 à 5, soit -4, et au passage on a aussi grâce à ce tableau les plus courts chemins de tous les nœuds allant à 5.
On remarque qu'à partir de l'étape 2 on n'effectue plus aucun changement sur le tableau, cela nous montre alors qu'on a trouvé notre solution dès l'étape 2 et il est tout à fait possible d'arrêter l'algorithme ici. Cependant, vu que la complexité en temps reste inchangé (dans le cas où le tableau est mis à jour à chaque étape), on n'implémentera pas cette amélioration afin de garder un code simple et concis.
Cette explication du pseudo-code nous permet d'introduire notre économie de mémoire qu'on cherchait à réaliser. En effet, dans ce tableau chaque ligne dépend de la précédente pour être calculée. Cela signifie que pour trouver la ligne 3, on a uniquement besoin de l'étape 2, et on peut donc se débarrasser de l'étape 0 et 1. Finalement, on se rend compte qu'on peut garder une ligne unique que l'on va mettre à jour à chaque étape puisqu'on n'a pas besoin de conserver plus que cela dans notre tableau. On a alors réussi à supprimer une dimension entière, et cela nous donne une complexité en mémoire de \(O(N)\). Cette amélioration nécessite quelques modifications dans notre pseudo-code, mais on va en profiter pour simplifier ce dernier :
Bellman-Ford :
plusCourtChemin[NB_NŒUD_MAX] (initialisé à -1)
plusCourtChemin[arrivée] = 0
Pour chaque étape
Pour chaque arc
cheminVoisin = pondérationArc + plusCourtChemin[nœud2arc]
plusCourtChemin[nœud1arc] = min(plusCourtChemin[nœud1arc], cheminVoisin)
Retourner plusCourtChemin[départ]En plus de réaliser une optimisation de l'espace mémoire, on facilite la lecture du pseudo-code en utilisant plus que deux boucles imbriquées à la place de trois. En effet, au lieu de parcourir les nœuds puis leurs voisins respectifs dans deux boucles imbriquées, on peut se contenter de visiter les arcs du graphe pour effectuer la même opération. Il ne faut pas oublier de lire le graphe en entrée comme une liste d'arcs pour permettre de parcourir tous les arcs en une seule boucle.
Notre pseudo-code n'est pas terminé, il nous reste encore la détection de cycles améliorants dans notre graphe, mais vu qu'on a simplifié et amélioré grandement notre pseudo-code, ce problème de cycles va être simple à gérer.
Pour détecter un cycle améliorant, il suffit de détecter si un chemin
emprunte plus de \(N\) nœuds, et on
peut très facilement réaliser ce test en regardant si le tableau
plusCourtChemin a été modifié une fois la limite atteinte
(on va donc réaliser un tour de boucle en plus). Si c'est le cas, on
sait que le graphe contient un cycle améliorant :
Bellman-Ford :
plusCourtChemin[NB_NŒUD_MAX] (initialisé à -1)
plusCourtChemin[arrivée] = 0
modification = faux
Pour chaque étape (avec un dernier tour de boucle en plus)
modification = faux
Pour chaque arc
cheminVoisin = pondérationArc + plusCourtChemin[nœud2arc]
Si cheminVoisin < plusCourtChemin[nœud1arc]
plusCourtChemin[nœud1arc] = cheminVoisin
modification = vrai
Si modification
Le graphe contient un cycle améliorant
Sinon
Retourner plusCourtChemin[départ]On a désormais le pseudo-code définitif de l'algorithme de Bellman-Ford.
L'avantage de passer de l'approche récursive à l'approche itérative dans un algorithme dynamique, est qu'on peut simplement trouver la complexité en temps de ce dernier. En effet, les deux boucles imbriquées nous permettent de calculer une complexité en temps de \(O(NM)\) avec \(N\) le nombre de nœuds du graphe, et \(M\) le nombre d'arcs (puisqu'on sait que pour éviter un cycle améliorant il suffit que \(K = N\)).
Cette complexité en temps est légèrement moins efficace que celle de l'algorithme de Dijkstra, mais reste raisonnable vu la complexité exponentielle de l'algorithme naïf. Surtout que l'algorithme de Dijkstra ne permet pas de réaliser le calcul du plus court chemin sur des graphes pondérés négativement, et que l'algorithme de Bellman-Ford gère le cas des cycles améliorants de manière très simple et élégante.
L'implémentation en C++ de l'algorithme de Bellman-Ford :
#include <cstdio>
#include <vector>
using namespace std;
struct Arc
{
int noeud1;
int noeud2;
int poids;
};
const int NB_NOEUD_MAX = 1000;
const int INFINI = 1000000000;
vector <Arc> arcs;
int nbNoeud, nbArc;
void bellmanFord(int depart, int arrivee)
{
int plusCourtChemin[NB_NOEUD_MAX];
int iEtape, iArc;
int iNoeud;
bool modification;
for(iNoeud = 0; iNoeud < NB_NOEUD_MAX; ++iNoeud)
plusCourtChemin[iNoeud] = INFINI;
plusCourtChemin[arrivee] = 0;
modification = false;
for(iEtape = 0; iEtape <= nbNoeud; ++iEtape) {
modification = false;
for(iArc = 0; iArc < arcs.size(); ++iArc) {
int noeud1, noeud2;
int cheminVoisin;
noeud1 = arcs[iArc].noeud1;
noeud2 = arcs[iArc].noeud2;
cheminVoisin = arcs[iArc].poids + plusCourtChemin[noeud2];
if(cheminVoisin < plusCourtChemin[noeud1]) {
plusCourtChemin[noeud1] = cheminVoisin;
modification = true;
}
}
}
if(modification)
printf("Cycle ameliorant !\n");
else
printf("%d\n", plusCourtChemin[depart]);
}
int main(void)
{
int depart, arrivee;
int iArc;
scanf("%d %d\n", &depart, &arrivee);
scanf("%d %d\n", &nbNoeud, &nbArc);
for(iArc = 0; iArc < nbArc; ++iArc) {
Arc nouveau;
scanf("%d %d %d\n", &nouveau.noeud1, &nouveau.noeud2, &nouveau.poids);
arcs.push_back(nouveau);
}
bellmanFord(depart, arrivee);
return 0;
}En entrée, on donne sur la première ligne le nœud de départ et d'arrivée pour le plus court chemin, puis sur la seconde ligne le nombre de nœuds et d'arcs du graphe, avant de terminer sur la liste d'arcs :
1 5
5 7
1 2 2
1 3 -1
2 3 3
2 4 -2
3 4 2
3 5 2
4 5 -4La sortie attendue sur le graphe précédemment étudié :
-4On teste avec notre exemple de graphe contenant un cycle améliorant :
1 4
4 5
1 2 -2
2 3 1
2 4 3
3 1 -2
3 4 -4Le cycle est bien détecté par l'algorithme :
Cycle ameliorant !L'algorithme de Bellman-Ford offre donc une toute nouvelle approche au problème du plus court chemin grâce à la programmation dynamique. Ceci lui permet d'être applicable sur tous types de graphes pondérés, contrairement à l'algorithme de Dijkstra qui n'est employé que sur des graphes pondérés positivement. De plus, le problème des cycles améliorants est facilement résolu avec cet algorithme, rendant le code simple et concis. En revanche, on notera une complexité en temps de \(O(NM)\), plus lente que celle de Dijkstra en \(O(M \log _2 M)\). Il est donc nécessaire de bien choisir l'algorithme à employer en fonction du graphe en entrée, afin d'avoir une complexité en temps et en mémoire optimale.
On a pu remarquer que l'algorithme de Bellman-Ford nous informe non seulement du plus court chemin entre le nœud de départ et le nœud d'arrivée, mais aussi des plus courts chemins de tous les autres nœuds vers celui d'arrivée. Mais que se passe-t-il si on désire connaître les plus courts chemins entre tous les nœuds du graphe ? Est-ce qu'on devrait réaliser \(N\) fois l'algorithme de Bellman-Ford ? Ou encore \(N\) fois l'algorithme de Dijkstra ? On se doute rapidement que cette méthode n'est pas efficace, et cette question est en réalité un problème à part entière dans la catégorie des plus courts chemins. On a alors su développer des algorithmes bien spécifiques à ce type de problème, comme l'algorithme de Floyd-Warshall, qui nous permet d'obtenir une complexité en temps plus intéressante. Connaître les plus courts chemins entre tous les nœuds d'un graphe est extrêmement utile dans de nombreux cas. On pourrait par exemple modéliser un problème de la vie de tous les jours sous forme d'un graphe implicite, afin de déterminer des relations ou des liens entre les différents nœuds.