Le principe du diviser pour régner est assez commun en algorithmique, et celui-ci repose sur une idée simple :
Il y a de nombreux domaines dans laquelle cette méthode excelle (dichotomie, tri fusion, tri rapide, etc.), mais là où elle atteint ses limites c'est lorsque les sous-problèmes rencontrés ne sont pas uniques. Dans ce cas, on en vient à recalculer beaucoup de sous-problèmes que l'on a déjà résolus, ce qui rend notre programme très lent, voire inutilisable.
La programmation dynamique est un moyen de pallier ce problème d'efficacité du programme, en stockant et en réutilisant les résultats déjà calculés pour éviter les nombreuses opérations inutiles. Plusieurs approches et techniques d'optimisation existent dans ce domaine, et nous étudierons dans cet article les principales.
Afin d'aborder cette notion le plus simplement possible, nous allons chercher à résoudre un problème concret, nous permettant de découvrir les différentes facettes de la programmation dynamique :
Envoyer des objets dans l'espace est une action très coûteuse. On estime qu'envoyer un kilo peut coûter entre 10.000$ et 20.000$ et même si ce prix diminue au fur et à mesure que de nouvelles méthodes de lancement sont mises en place, il est nécessaire de minimiser le coût de chaque opération.
Vous travaillez pour l'entreprise chargée du prochain ravitaillement de la Station Spatiale Internationale, votre rôle va être de préparer le contenu du prochain lanceur. Votre équipe a réuni \(N\) objets (cela peut être de la nourriture, du carburant, du nouveau matériel, des expériences scientifiques à mener, etc.), et possède à disposition un lanceur pouvant contenir au maximum \(M\) kilos. Chaque objet sera décrit selon deux caractéristiques :
- Son poids \(p\) en kilo (avec \(0 < p <= M\))
- Son importance \(i\) pour la mission (avec \(0 < i < 50\))
Afin de rentabiliser au mieux les coûts du lancement, vous êtes demandé de trouver un arrangement d'objets tel que l'importance cumulée de ces derniers (notée \(I\)) soit maximale, tout en faisant attention à ne pas dépasser les \(M\) kilos supportés par le lanceur.
Toutes les données fournies en entrée (\(N\), \(M\), \(p\), \(i\)) sont des nombres entiers.
Lorsqu'on est face à un problème, il est fondamental d'essayer quelques exemples simples à la main pour être certain d'avoir entièrement compris le sujet donné, mais aussi pour commencer à réfléchir sur la solution.
Imaginons l'exemple suivant :
| Objet | Poids | Importance |
|---|---|---|
| 1 | 160 | 45 |
| 2 | 60 | 25 |
| 3 | 65 | 25 |
| 4 | 20 | 30 |
| 5 | 40 | 10 |
Avec \(N = 5\) et \(M = 180\).
Voici quelques idées qui peuvent nous venir en tête lorsqu'on cherche à résoudre cet exemple :
On ne peut pas trouver un autre arrangement d'objets avec une importance totale supérieure à 80, c'est donc notre réponse.
Cet exemple permet de faire ressortir plusieurs informations cruciales à propos de ce problème. Tout d'abord, les deux premières idées qui peuvent paraître intéressantes et logiques, ne fournissent pas toujours une solution optimale comme on vient de le voir. Trier les objets en fonction de leurs caractéristiques n'est donc pas un algorithme valide. Aussi, on a résolu le problème avec plus d'intuition que de logique pure, car chercher des objets moyens n'est pas du tout précis et loin d'être un algorithme d'ordre général. Si l'on devait recommencer sur un exemple avec davantage d'objets (supposons \(N = 30\)), cela deviendrait vite impossible de trouver intuitivement la solution, et même si l'on établissait des règles pour décrire un objet moyen, il serait très facile de trouver un nouveau contre exemple à chaque fois.
Ce qui nous bloque dans nos recherches c'est que l'on essaie de faire deux choses à la fois : résoudre le problème et le faire intelligemment. Et si on commençait tout simplement par résoudre le problème, avant de se soucier de l'efficacité ?
Afin de se concentrer sur l'algorithme, nous allons utiliser un énoncé simplifié dans lequel on nous demande uniquement l'importance maximale et non plus l'arrangement d'objet associé. L'arrangement en lui-même est en réalité un détail du problème, et nous verrons à la fin qu'il est tout à fait possible de le retrouver à partir de nos résultats.
Un algorithme dit naïf a pour unique but de résoudre un problème de manière très simple, sans se préoccuper de la complexité en temps et en mémoire.
Dans notre exemple de fusée, un algorithme naïf pourrait être de tester chaque arrangement d'objets possible ne posant pas de problème de surcharge, et de garder celui qui maximise l'importance des objets :
maximiser_importance():
importance_max = 0
Pour chaque arrangement d'objets
Si importance > importance_max ET pas de surcharge
importance_max = importance
Retourner importance_max
Afficher maximiser_importance()Ce pseudo-code est tellement trivial que vous vous demandez surement quelle est son utilité. Pourtant, partir d'un algorithme naïf lorsqu'on n'a pas d'idées de solution efficace est souvent un bon point de départ. En effet, ces types d'algorithme sont évidents à trouver, et le pseudo-code associé est la plupart du temps court, simple et sans bug. De plus, si on a besoin de l'améliorer, on peut résoudre à la main un exemple avec l'algorithme, ce qui soulignera rapidement ses points faibles et nous indiquera les parties à optimiser.
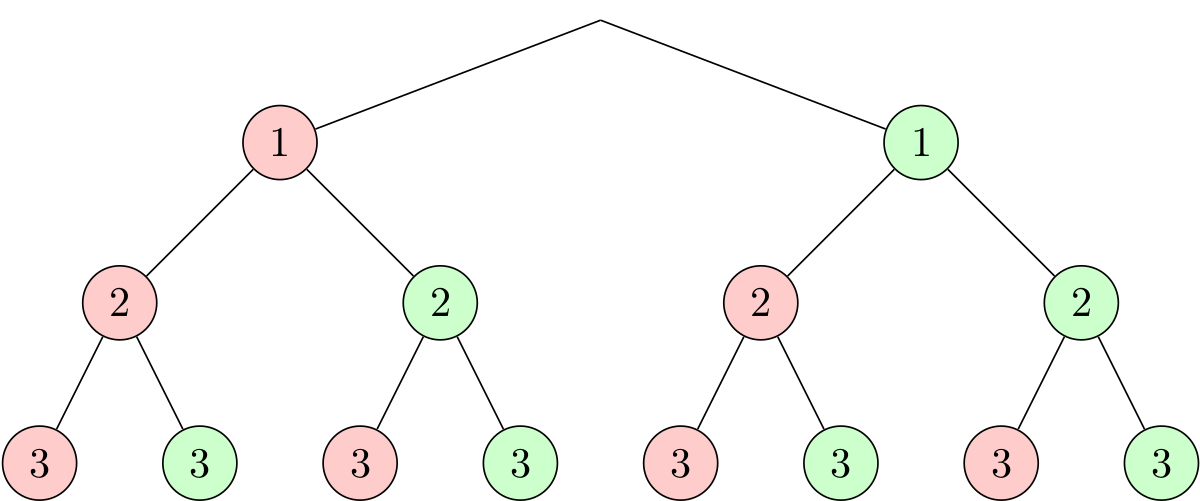
Pour faciliter l'implémentation, détaillons davantage le pseudo-code car la partie qui énumère les différents arrangements d'objets reste assez imprécise. On peut partir d'un principe très simple : pour chaque objet, on a le choix entre soit le prendre dans la fusée, soit le laisser sur Terre. Imaginons que notre énoncé nous fournisse 3 objets, on pourrait représenter les différents choix grâce à un arbre :

Chaque nœud correspond à un objet, et sa couleur détermine si on le
prend (vert) ou si on le laisse (rouge). Toutes les possibilités sont
énumérées ici (on imagine dans notre exemple qu'on n'a pas de problème
de surpoids afin de bien visualiser l'arbre en entier). La ligne
Pour chaque arrangement d'objets de notre pseudo-code
devient alors Pour chaque chemin de l'arbre. Parcourir un
arbre est une opération très simple, et on peut utiliser différentes
méthodes comme le parcours
en profondeur ou encore le parcours
en largeur.
Dans notre cas, le parcours en profondeur semble le plus adapté. On peut alors détailler davantage notre pseudo-code qui suit désormais une approche récursive :
maximiser_importance(index_objet, poids_dispo):
Si index_objet > nb_objets
Retourner 0
prend_pas_objet = maximiser_importance(index_objet + 1, poids_dispo)
Si objet.poids <= poids_dispo
prend_objet = objet.importance +
maximiser_importance(index_objet + 1, poids_dispo - objet.poids)
Sinon
prend_objet = 0
Retourner max(prend_pas_objet, prend_objet)
Afficher maximiser_importance(1, poids_max)Plusieurs choses à noter sur ce pseudo-code :
maximiser_importance résout le problème
suivant : Quel est l'importance maximale que l'on peut atteindre en
ayant uniquement à disposition les objets d'indice
index_objet à \(N\), et
sans dépasser poids_dispo ? Notre algorithme naïf consiste
donc à maximiser les réponses de chaque sous-problème, pour résoudre
notre problème original.Il est nécessaire de bien appréhender ce pseudo-code de l'algorithme naïf, avant de l'implémenter et de l'optimiser.
Un exemple d'implémentation en C :
#include <stdio.h>
#define NB_OBJETS_MAX 1000
struct Objet {
int poids;
int importance;
};
struct Objet objets[NB_OBJETS_MAX];
int nb_objets;
int poids_max;
int max(int a, int b)
{
if(a > b)
return a;
else
return b;
}
int maximiser_importance(int index_objet, int poids_dispo)
{
if(index_objet > nb_objets)
return 0;
struct Objet objet = objets[index_objet];
int prend_pas_objet, prend_objet;
/* Choix 1 */
prend_pas_objet = maximiser_importance(index_objet + 1, poids_dispo);
/* Choix 2 */
if(objet.poids <= poids_dispo)
prend_objet = objet.importance +
maximiser_importance(index_objet + 1, poids_dispo - objet.poids);
else
prend_objet = 0;
return max(prend_objet, prend_pas_objet);
}
int main(void)
{
int iObjet;
/* Récupère les données fournies en entrée */
scanf("%d %d\n", &nb_objets, &poids_max);
for(iObjet = 1; iObjet <= nb_objets; ++iObjet)
scanf("%d %d\n", &objets[iObjet].poids, &objets[iObjet].importance);
printf("%d\n", maximiser_importance(1, poids_max));
return 0;
}J'utilise des variables globales pour les structures principales du programme car cela facilite l'écriture et la lecture, sans pour autant poser de problèmes puisque le code tient dans un seul fichier très court.
En reprenant notre exemple initial, on peut fournir en entrée du programme :
5 180
160 45
60 25
65 25
20 30
40 10Sur la première ligne on a \(N\) puis \(M\), et sur les \(N\) prochaines lignes, le poids et l'importance de chaque objet.
On obtient bien en sortie :
1 2 3
80Vous êtes très fier de votre programme, et vous réussissez avec succès à résoudre votre problème de cargo. Cependant, quelques jours plus tard, votre supérieur vous informe que les objets envoyés ne viendront pas uniquement de la société dans laquelle vous travaillez, mais aussi d'autres entreprises (après tout, l'ISS est un effort international, cela paraît donc logique). A première vue, vous n'y voyez aucun problème car il suffit de refaire tourner le programme avec la nouvelle liste d'objets (plus conséquente du coup). Mais votre programme ne semble jamais se terminer...
Réalisons quelques tests du programme sur différentes tailles d'entrée :
| Taille entrée (\(N\)) | Temps d'exécution |
|---|---|
| 10 | 0.00s |
| 20 | 0.02s |
| 25 | 0.55s |
| 30 | 14.66s |
| 35 | 7min48s |
| 40 | 4h10min |
Bien sûr, les résultats varient en fonction de l'ordinateur qui exécute le programme, mais même en utilisant des superordinateurs, une liste de quelques centaines voire milliers d'objets paralyserait totalement le programme qui nécessitera alors une infinité de temps pour résoudre le problème. Ceci est dû à la croissance exponentielle de notre algorithme.
Les tests ont été réalisés sur des entrées sans problème de surcharge pour faire ressortir au mieux cette croissance exponentielle, mais même avec des entrées comprenant des arrangements d'objets en surpoids, le problème reste identique.
En effet, avec \(N\) objets et 2 choix possibles pour chacun, on a dans le pire des cas \(2^N\) branches à explorer. Même avec les problèmes de surpoids qui diminuent le nombre de possibilités, on se rapproche fatalement de \(2^N\) lorsque \(N\) est grand.
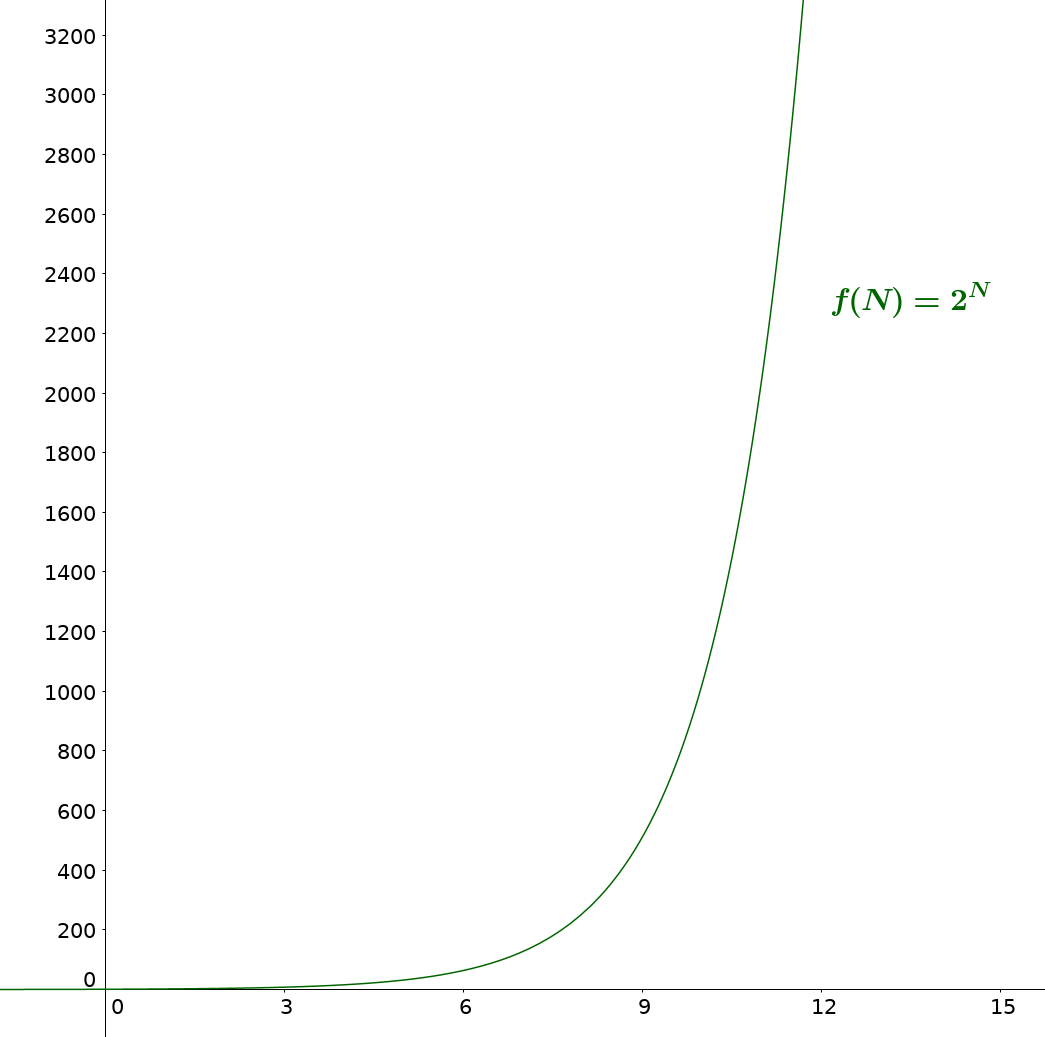
Il n'est pas du tout envisageable d'utiliser concrètement un programme avec une complexité en temps de \(O(2^N)\), il faut donc améliorer notre algorithme.
Comme nous l'avons vu, un algorithme naïf a pour avantage de facilement faire ressortir ses inconvénients lorsqu'on réalise un exemple à la main avec ce dernier. Prenons un nouvel exemple où il n'y a pas de problème de surpoids (pour mieux visualiser l'arbre complet) afin d'identifier facilement les répétitions inutiles de notre algorithme :
| Poids | Importance |
|---|---|
| 20 | 10 |
| 20 | 15 |
| 10 | 5 |
| 25 | 15 |
| 5 | 5 |
Avec \(N = 5\) et \(M = 150\).
Si l'on représente les appels récursifs et les paramètres de ces derniers, on obtient l'arbre suivant :
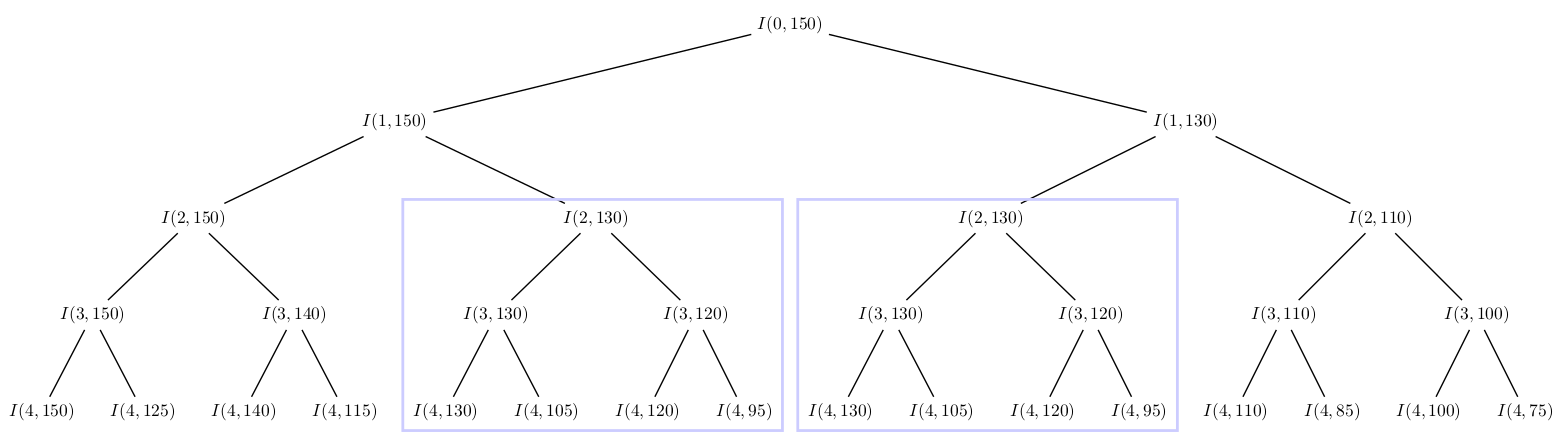
On voit rapidement que des appels récursifs sont répétés, et notamment tout un sous-arbre dans ce cas. Or, chaque appel récursif correspond à la réponse d'un sous-problème, notre algorithme recalcule donc sans cesse des solutions aux mêmes sous-problèmes. Plus \(N\) est important, plus ces répétitions sont fréquentes et c'est ce qui cause la lenteur si extrême de notre programme.
Pour se donner une idée de l'omniprésence de ces répétitions inutiles, voici quelques statistiques. Chaque résultat représente une moyenne sur 50 entrées aléatoires (avec la possibilité de surpoids) :
| Taille entrée (\(N\)) | Pourcentage de répétition |
|---|---|
| 10 | 15% |
| 15 | 32% |
| 20 | 63% |
| 25 | 77% |
| 30 | 87% |
| 35 | 94% |
À noter que sans problème de surcharge, on atteint plus de 90% de répétition dans les appels dès :math:`N = 15`.
La programmation dynamique (dynamic programming ou encore dynamic optimization en anglais) est une technique d'optimisation d'un algorithme visant à éviter de recalculer des sous-problèmes en stockant les résultats en mémoire. L'idée est simple, mais le gain sur la complexité en temps peut être considérable, et cette technique est très largement utilisée dans de nombreux algorithmes. Cette technique de programmation suit le principe d'optimalité de Bellman énonçant que la solution optimale d'un problème peut être calculée à partir de solutions optimales de sous-problèmes (Richard Bellman étant un des pères fondateurs de la programmation dynamique).
En réalité, vous utilisez cette optimisation très souvent sans même vous en rendre compte. Si je vous demande de me calculer le résultat de "1 + 1 + 1 + 1 + 1 + 1 + 1 + 1" vous mettrez un certain temps afin de trouver la somme des termes, mais si je rajoute "+ 1" à la fin de ce calcul, vous pouvez me répondre instantanément le résultat de la nouvelle expression. Vous avez naturellement stocké en mémoire le résultat de l'expression originale, que vous avez ensuite réutilisé pour trouver le résultat d'une nouvelle expression sans avoir besoin de refaire le calcul en entier.
Voici une version dynamique de notre pseudo-code :
importance_max[nb_objets_max][poids_max] initialisé à PAS_CALCULÉ
maximiser_importance(index_objet, poids_dispo):
Si index_objet > nb_objets
Retourner 0
Si importance_max[index_objet][poids_dispo] != PAS_CALCULÉ
Retourner importance_max[index_objet][poids_dispo]
prend_pas_objet = maximiser_importance(index_objet + 1, poids_dispo)
Si objet.poids <= poids_dispo
prend_objet = objet.importance +
maximiser_importance(index_objet + 1, poids_dispo - objet.poids)
Sinon
prend_objet = 0
importance_max[index_objet][poids_dispo] = max(prend_pas_objet, prend_objet)
Retourner importance_max[index_objet][poids_dispo]
Afficher maximiser_importance(1, poids_max)Plusieurs changements par rapport à l'algorithme naïf non dynamisé :
importance_max de taille \(N\)x\(M\)
qui stockera toutes les solutions des sous-problèmes que l'on va
résoudre avec notre récursion. Il est important de ne pas oublier de
l'initialiser correctement.Le cœur de l'algorithme est inchangé, on a toujours nos deux choix, ainsi que nos conditions d'arrêts (plus aucun objet à prendre ou problème de surcharge), mais on gère bien plus intelligemment nos résultats en les stockant en mémoire pour éviter de les recalculer : on parle de mémoïsation.
Une implémentation en C de la version dynamisée de l'algorithme :
#include <stdio.h>
#define NB_OBJETS_MAX 1000
#define POIDS_MAX 1000
#define PAS_CALCULE -1
struct Objet {
int poids;
int importance;
};
struct Objet objets[NB_OBJETS_MAX];
int nb_objets;
int poids_max;
int importance_max[NB_OBJETS_MAX][POIDS_MAX];
int max(int a, int b)
{
if(a > b)
return a;
else
return b;
}
int maximiser_importance(int index_objet, int poids_dispo)
{
if(index_objet > nb_objets)
return 0;
/* On vérifie qu'on n'a pas déjà calculé ce résultat */
if(importance_max[index_objet][poids_dispo] != PAS_CALCULE)
return importance_max[index_objet][poids_dispo];
struct Objet objet = objets[index_objet];
int prend_pas_objet, prend_objet;
/* Choix 1 */
prend_pas_objet = maximiser_importance(index_objet + 1, poids_dispo);
/* Choix 2 */
if(objet.poids <= poids_dispo)
prend_objet = objet.importance +
maximiser_importance(index_objet + 1, poids_dispo - objet.poids);
else
prend_objet = 0;
/* On garde en mémoire le résultat avant de le retourner */
importance_max[index_objet][poids_dispo] = max(prend_objet, prend_pas_objet);
return importance_max[index_objet][poids_dispo];
}
int main(void)
{
int iObjet, iPoids;
/* Récupère les données fournies en entrée */
scanf("%d %d\n", &nb_objets, &poids_max);
for(iObjet = 1; iObjet <= nb_objets; ++iObjet)
scanf("%d %d\n", &objets[iObjet].poids, &objets[iObjet].importance);
/* Initialise notre tableau de résultats */
for(iObjet = 1; iObjet <= nb_objets; ++iObjet)
for(iPoids = 0; iPoids <= poids_max; ++iPoids)
importance_max[iObjet][iPoids] = PAS_CALCULE;
printf("%d\n", maximiser_importance(1, poids_max));
return 0;
}Ces quelques légères modifications de notre code ont un impact colossal sur la complexité en temps de notre algorithme :
| Taille entrée (\(N\)) | Temps d'exécution |
|---|---|
| 10 | 0,00s |
| 100 | 0,00s |
| 1000 | 0,09s |
| 10000 | 2,47s |
Cependant, comment savoir quelle forme doit prendre notre algorithme récursif pour le dynamiser correctement ? En effet, on aurait pu coder l'algorithme naïf totalement différemment, et il est donc important de comprendre et connaître quelques caractéristiques fondamentales d'un code récursif que l'on cherche à dynamiser à l'aide de la mémoïsation :
index_objet à \(N\) sans dépasser
poids_dispo).La programmation dynamique est l'exemple parfait de compromis entre complexité en temps et complexité en mémoire. En effet, en stockant nos résultats, et donc en augmentant la complexité en mémoire, on arrive à réduire radicalement la complexité en temps. Dans notre cas, l'optimisation est très intéressante car elle permet d'éviter une complexité en temps exponentielle qui rendait notre programme inutilisable, sans pour autant saturer totalement la mémoire disponible. Cependant, ce n'est pas toujours le cas et il arrive que la complexité en mémoire augmente tellement que le compromis n'est plus envisageable, mais il est possible de réduire intelligemment l'espace mémoire occupé par de nombreux algorithmes dynamiques.
Afin d'introduire cette nouvelle optimisation de mémoire, il est nécessaire de changer dans un premier temps notre approche de résolution. Avec l'algorithme récursif, nous utilisions une méthode dite descendante (ou top-down) en partant du problème que l'on cherchait à résoudre et en le découpant en sous-problème, d'où la notion de descente. Le principal inconvénient de cette méthode est qu'on ne peut pas se débarrasser des calculs intermédiaires car la résolution du problème final dépend nécessairement de la résolution de ces sous-calculs qui eux même dépendent directement de la résolution de sous-sous-calculs et ainsi de suite. Les différentes informations sont alors indispensables à cause de ces liens de dépendance très forts entre les calculs. En revanche, si l'on adopte une nouvelle méthode dite ascendante (ou bottom-up), on peut imposer un ordre de résolution différent, permettant ainsi de commencer par les sous-problèmes les plus basiques puis de monter en complexité jusqu'à résoudre le problème original, d'où la notion d'ascension. L'avantage de cette méthode est que les liens de dépendance entre les calculs sont beaucoup plus faibles, on peut alors se permettre de stocker uniquement les éléments servant à résoudre le prochain problème, et donc se débarrasser de la plupart des anciens sous-problèmes qui ne nous servent plus pour avancer.
La première étape de notre optimisation consiste donc à transformer
notre algorithme dynamique récursif (méthode descendante) en un
algorithme dynamique itératif (méthode ascendante). On
a notre tableau importance_max[nb_objets_max][poids_max] à
deux dimensions, qui représente l'importance maximale que l'on peut
avoir en utilisant certains objets sans dépasser un certain poids. Notre
objectif est donc de remplir la case
(nb_objets;poids_max) du tableau car c'est
elle qui correspond à la solution de notre problème original. En
utilisant une approche ascendante il faut donc commencer par la case
(0;0), et remplir le tableau jusqu'à la case
(nb_objets;poids_max) à l'aide de boucles.
Cependant, que faut-il mettre dans la case (0;0) ? En effet, avec la méthode ascendante on commence par des cas très simples à traiter qu'on est censé pouvoir résoudre sans avoir besoin d'information au préalable. Remplir la case (0;0) revient à résoudre le problème suivant : quelle est l'importance maximale que l'on peut avoir en utilisant 0 objet sans dépasser 0 kg ? La réponse est évidemment 0, et on remarque que l'on peut remplir de la même façon toutes les cases (0;\(y\)) à 0 (avec \(y\) variant de 0 à \(M\)). Nous avons donc rempli la première ligne de notre tableau, qui va nous servir à calculer progressivement les suivantes. Pour cela, il faut s'appuyer sur notre récurrence, car même si l'approche change, la relation de dépendance entre les sous-problèmes reste quasiment identique. Linéariser l'algorithme peut être difficile si la relation de récurrence n'a pas été correctement définie au préalable. Afin de mieux visualiser ces différents liens entre les cases du tableau, on peut s'appuyer sur une méthode très utile et rapidement indispensable de France-IOI qui consiste à réaliser un schéma indiquant les cas de bases, la dépendance des calculs et enfin le calcul final désiré :
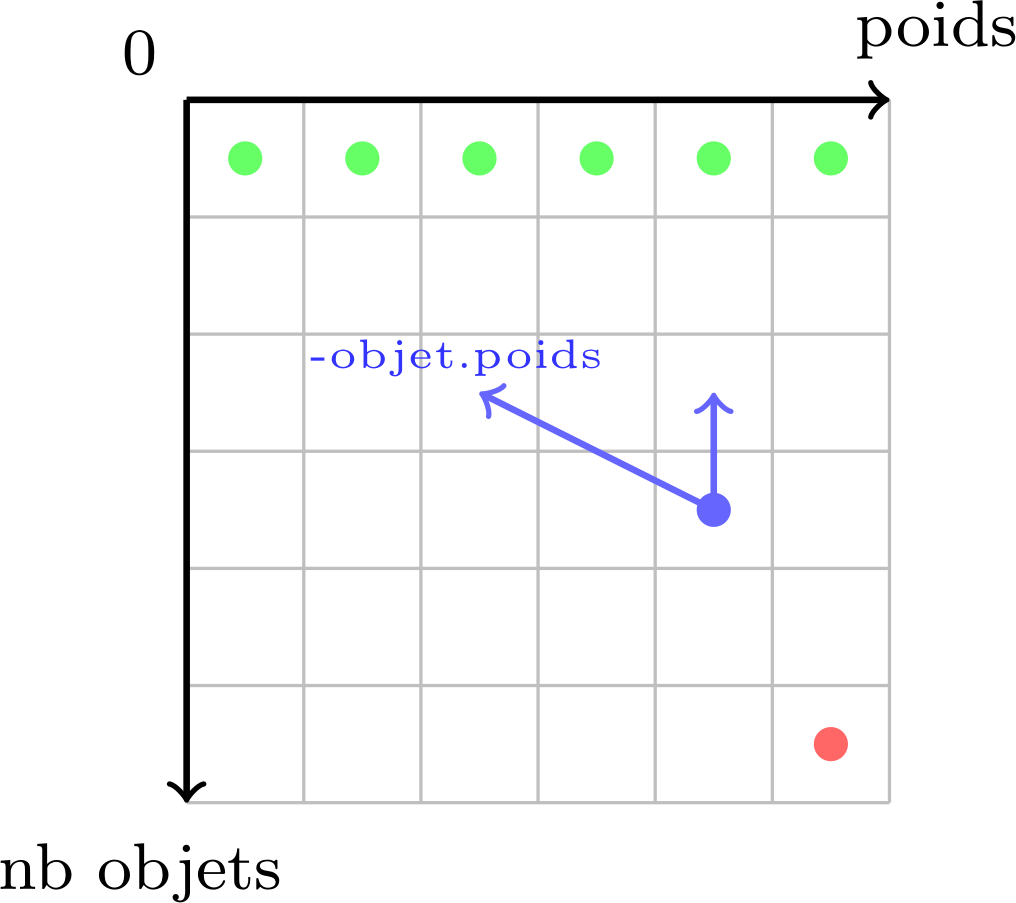
Ce schéma est une représentation graphique de notre tableau à deux
dimensions, où chaque case stocke la solution à un sous-problème
spécifique (la ligne d'une case correspond au nombre d'objets utilisé
pour résoudre ledit problème, et la colonne au poids disponible). En
vert, on retrouve nos différents cas de bases à la ligne 0, en bleu un
exemple des liens de dépendance, et en rouge notre objectif final. Le
point bleu signifie que la case applique une fonction (dans notre cas
max) aux valeurs des cases pointées par les flèches bleues.
Ces deux flèches représentent les deux choix qu'on a pour chaque objet
:
objet.poids, et on actualise l'importance
maximale en ajoutant celle de l'objet au résultat du précédent
sous-problème (sur le schéma, la première flèche pointe vers une case
arbitraire pour montrer qu'elle dépend d'un paramètre précis, ici le
poids de l'objet, contrairement au cas où on ne prend pas l'objet où la
flèche pointe directement vers la case du dessus).Pour gérer le cas de la surcharge, on fait exactement comme dans le cas où on ne prend pas l'objet, c'est-à-dire qu'on réutilise la solution du problème précédent.
Le pseudo-code de l'algorithme itératif ressemble donc à ceci :
importance_max[nb_objets][poids_max]
maximiser_importance():
Pour chaque poids
importance_max[0][iPoids] = 0
Pour chaque objet
Pour chaque poids
prend_pas_objet = importance_max[iObjet - 1][iPoids]
Si objet.poids <= iPoids
prend_objet = objet.importance +
importance_max[iObjet - 1][iPoids - objet.poids]
Sinon
prend_objet = 0
importance_max[iObjet][iPoids] = max(prend_objet, prend_pas_objet)
Retourner importance_max[nb_objets][poids_max]La première boucle correspond à la résolution des cas de bases, puis
on a deux boucles imbriquées qui permettent de parcourir chaque case du
tableau. La relation de dépendance des calculs est quasiment identique à
notre relation de récurrence, excepté qu'on utilise une approche
ascendante donc on se sert des résultats précédents (d'où le
iObjet - 1), alors que dans une approche descendante on
cherchait à découper le problème (d'où le index_objet + 1
dans nos pseudo-code récursifs). Ici, on ne parle plus de mémoïsation
mais de tabulation.
Cependant, l'optimisation que l'on cherche à réaliser avec cette
nouvelle approche concerne la complexité en mémoire. À partir de la
version itérative, on remarque une chose très importante : chaque case
du tableau importance_max dépend uniquement de la ligne
précédente. Ceci signifie qu'à tout moment on a besoin de deux lignes
dans notre tableau :
On peut alors "recycler" sans cesse ces deux lignes pour passer d'une complexité en mémoire de \(O(NM)\) (version récursive et itérative non optimisée) à \(O(2M)\) qu'on peut se permettre de simplifier en \(O(M)\) (car lorsque \(M\) est très grand, le facteur 2 n'impacte quasiment pas le résultat). Pour alterner entre les deux lignes du tableau, on peut par exemple utiliser la parité des index (si l'index utilisé est pair, on stocke les résultats actuels dans la première ligne, sinon on stocke dans la deuxième ligne). Ceci permet de diminuer sévèrement notre consommation de mémoire en changeant très peu de code :
importance_max[2][poids_max]
maximiser_importance():
Pour chaque poids
importance_max[0][iPoids] = 0
Pour chaque objet
Pour chaque poids
prend_pas_objet = importance_max[(iObjet - 1) mod 2][iPoids]
Si objet.poids <= iPoids
prend_objet = objet.importance +
importance_max[(iObjet - 1) mod 2][iPoids - objet.poids]
Sinon
prend_objet = 0
importance_max[iObjet mod 2][iPoids] = max(prend_objet, prend_pas_objet)
Retourner importance_max[nb_objets mod 2][poids_max]Notre déclaration du tableau importance_max prend
désormais en compte les deux lignes uniquement nécessaires, et l'ajout
de l'opération modulo 2 permet l'alternance entre ces
dernières à l'aide de la parité des index.
Une version en C de l'algorithme dynamique itératif et optimisé :
#include <stdio.h>
#define NB_OBJETS_MAX 1000
#define POIDS_MAX 1000
#define PAS_CALCULE -1
struct Objet {
int poids;
int importance;
};
struct Objet objets[NB_OBJETS_MAX];
int nb_objets;
int poids_max;
int importance_max[2][POIDS_MAX];
int max(int a, int b)
{
if(a > b)
return a;
else
return b;
}
int maximiser_importance(void)
{
int iObjet, iPoids;
/* Résolution des cas de bases */
for(iPoids = 0; iPoids <= poids_max; ++iPoids)
importance_max[0][iPoids] = 0;
/* On remplit toutes les cases du tableau */
for(iObjet = 1; iObjet <= nb_objets; ++iObjet) {
for(iPoids = 0; iPoids <= poids_max; ++iPoids) {
struct Objet objet = objets[iObjet];
int prend_pas_objet, prend_objet;
/* Choix 1 */
prend_pas_objet = importance_max[(iObjet - 1) % 2][iPoids];
/* Choix 2 */
if(objet.poids <= iPoids)
prend_objet = objet.importance +
importance_max[(iObjet - 1) % 2][iPoids - objet.poids];
else
prend_objet = 0;
importance_max[iObjet % 2][iPoids] = max(prend_objet, prend_pas_objet);
}
}
return importance_max[nb_objets % 2][poids_max];
}
int main(void)
{
int iObjet;
/* Récupère les données fournies en entrée */
scanf("%d %d\n", &nb_objets, &poids_max);
for(iObjet = 1; iObjet <= nb_objets; ++iObjet)
scanf("%d %d\n", &objets[iObjet].poids, &objets[iObjet].importance);
printf("%d\n", maximiser_importance());
return 0;
}Il est néanmoins important de noter que cette solution n'est pas forcément la meilleure, car même si la complexité en mémoire a été très largement amélioré, la complexité en temps des précédents algorithmes itératifs est théoriquement plus importante que celle de l'algorithme récursif. En effet, l'approche ascendante nécessite de calculer la solution de tous les sous-problèmes possibles (c'est-à-dire remplir entièrement le tableau), là où l'algorithme récursif se contente de résoudre uniquement les sous-problèmes dont il a besoin. L'utilisation du mot "théoriquement" n'était pas en vain, car en pratique, l'algorithme récursif est ralenti au fur et à mesure que la taille de l'entrée augmente à cause d'une surcharge de la pile d'appel, ce qui n'arrive pas avec la version itérative. On observe parfaitement ce phénomène en comparant des tailles d'entrées différentes :
| Taille entrée (\(N\)) | Dynamique récursif | Dynamique itératif |
|---|---|---|
| 10 | 0,00s | 0,00s |
| 100 | 0,00s | 0,02s |
| 1000 | 0,09s | 0,17s |
| 10000 | 2,47s | 1,44s |
L'algorithme récursif semble plus efficace pour des entrées de taille inférieure à 1000, mais prend un retard non négligeable avec une entrée de taille 10000 à cause de cette accumulation d'appels récursifs. L'implémentation d'un algorithme dynamique dépend donc énormément du problème posé, et des contraintes qu'on cherche à satisfaire (complexité en temps et en mémoire), d'où l'importance de connaître les avantages et les inconvénients de chaque méthode.
Au début de cet article, nous avions simplifié le problème pour se concentrer uniquement sur l'aspect de la programmation dynamique, sans prendre la peine d'afficher en sortie du programme la liste d'objets choisie pour maximiser l'importance totale. Cette liste est en réalité un détail que l'on peut retrouver assez facilement, mais cet ajout soulève un nouveau problème d'optimisation. En effet, en cherchant à avoir davantage de détails sur la solution du problème, il nous faut plus d'informations dans lesquelles chercher, et dans notre cas cela nous empêche de réaliser l'optimisation en mémoire qu'on a évoqué précédemment. À nouveau, on remarque comment un changement dans l'énoncé peut impacter fortement notre implémentation de l'algorithme dynamique ainsi que ses performances et les contraintes qu'on cherche à respecter.
À l'aide de l'algorithme itératif non optimisé, trouver la liste
d'objets est une étape très facile, qu'on peut réaliser sans avoir
besoin de stocker des données supplémentaires et en utilisant uniquement
notre tableau à deux dimensions importance_max :
afficher_liste_objets():
iObjet = nb_objets
iPoids = poids_max
Tant que iObjet > 0
Si importance_max[iObjet][iPoids] > importance_max[iObjet - 1][iPoids]
L'objet d'indice iObjet est dans la liste
iPoids -= objets[iObjet].poids
--iObjetL'idée est simple, on part de la solution, c'est-à-dire la case
(nb_objets;poids_max) du tableau, et on
remonte le chemin emprunté en suivant un principe basé sur notre
relation de dépendance : s'il y a une différence d'importance entre la
case actuelle et celle juste au-dessus (qui représente, comme nous
l'avons vu, le cas où on ne prend pas l'objet), alors c'est qu'on a
nécessairement pris un nouvel objet dans la fusée (ce dernier étant
d'indice iObjet). On continue la recherche en prenant soin
d'actualiser le poids disponible, et on s'arrête lorsqu'on a passé en
revu tous les objets possibles.
La programmation dynamique est donc une technique d'optimisation visant à diminuer considérablement la complexité en temps d'algorithmes en évitant de recalculer sans cesse les mêmes résultats. L'exemple que nous avons traité durant cet article est plus connu sous le nom de problème du sac à dos, et il nous a permis d'étudier différentes facettes et techniques d'optimisation que nous apporte la programmation dynamique :
Ce qui est vital de retenir est qu'aucune des deux approches n'est meilleure que l'autre, et qu'il faut s'adapter à la situation, au problème posé et aux contraintes à respecter. C'est ce qui rend la programmation dynamique si difficile à appréhender et à mettre en place, surtout lorsqu'on débute avec les algorithmes. Une bonne méthode pour commencer à utiliser les algorithmes dynamiques serait de procéder par étape :
Avec l'expérience, il est éventuellement possible de choisir dès le début l'approche que l'on va mettre en place pour résoudre le problème, mais il faut bien anticiper car en fonction du sujet une méthode peut être plus simple à comprendre ou à coder que l'autre, ou encore ne pas respecter les contraintes données.
Il est important de noter que cet article constitue une simple introduction à la matière, et non une liste exhaustive de toutes les techniques et optimisations de programmation dynamique. Il n'y a pas de secret, et pour être réellement à l'aise avec ce domaine il est nécessaire de pratiquer énormément sur des sujets variés, car des problèmes de programmation dynamique peuvent être formulés de nombreuses manières. Je vous invite donc à pousser davantage vos recherches sur le sujet, car il y a beaucoup d'informations et de ressources en ligne. Voici quelques liens qui peuvent vous aider :
Cet article a aussi été publié sur `Zeste de Savoir <https://zestedesavoir.com/>`__, je tiens donc à remercier les membres qui m'ont fait part de leurs retours, en particulier `yoch <https://zestedesavoir.com/membres/voir/yoch/>`__ pour ses différentes remarques et relectures.