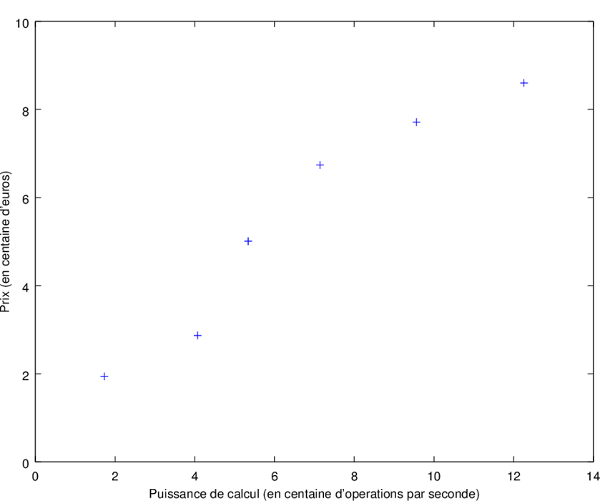
Vous souhaitez estimer le prix d'un ordinateur en fonction de différents facteurs (puissance, mémoire, stockage, batterie, etc.), cependant la tâche se complique au fur et à mesure que vous rajoutez des possibilités, et vous décidez alors d'employer un algorithme d'apprentissage artificiel pour faire le travail à votre place. Afin de prendre un exemple simple, on va dire que vous estimez le prix d'un ordinateur uniquement en fonction de sa puissance de calcul. Dans l'introduction à la matière, on a vu que récolter des données utiles est une étape importante dans un processus d'apprentissage, et vous avez alors noté la puissance et le prix de différents ordinateurs dans un tableau :
Les données sont totalement inventées et ne servent que d'exemple.
| Puissance (nombre d'opérations/s) | Prix (€) |
|---|---|
| 173 | 194 |
| 407 | 287 |
| 534 | 501 |
| 714 | 674 |
| 956 | 771 |
| 1226 | 860 |
On peut représenter ce tableau grâce à un graphique en deux dimensions très simple :

Ce qu'on cherche à faire dans notre problème c'est d'**extrapoler**, c'est-à-dire généraliser grâce aux données obtenues afin de prédire un résultat. En tant qu'humain, on pourrait facilement faire une bonne généralisation comme ceci :
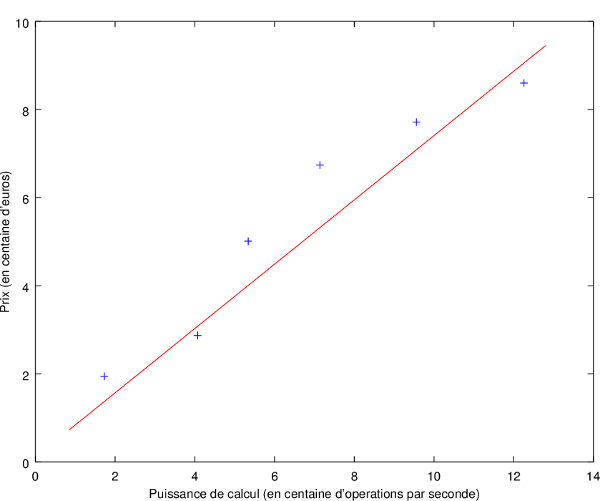
On a une fonction linéaire basique, qu'on peut ensuite utiliser graphiquement pour trouver à partir de la puissance d'un ordinateur, une bonne estimation de son prix.
Cependant, du point de vue d'une personne, il est facile de trouver un lien entre les données dans le but de généraliser, mais comment un algorithme peut-il reproduire ce comportement ? Qu'est-ce qui fait qu'une fonction (linéaire, polynomiale, etc.) est une bonne généralisation de notre problème ?
Avant de se lancer dans la recherche d'un algorithme d'apprentissage artificiel, il faut définir ses caractéristiques. Dans notre problème, on a un ensemble de données sous la forme d'entrées et de sorties correspondantes, nous sommes donc dans un apprentissage supervisé. De plus, la sortie qu'on cherche est une valeur numérique, notre problème appartient alors au domaine de la régression. Une fois qu'on connaît ces deux informations essentielles, on peut décider de l'algorithme à utiliser en fonction de nos besoins et de nos ressources. Dans notre situation on souhaiterait faire une généralisation sous la forme d'une fonction linéaire, la méthode à employer est donc : la régression linéaire.
La régression linéaire n'est qu'un cas particulier de la régression polynomiale, mais il est plus simple de commencer avec une simple fonction linéaire pour ensuite aborder des fonctions plus complexes (même si le principe reste exactement le même).
La régression linéaire est un moyen de généraliser et de créer un modèle linéaire à partir d'exemples. Lesdits exemples sont représentés à l'aide de matrices où \(x\) est l'entrée, et \(y\) est la sortie correspondante. Prenons le cas où on essaie de généraliser le prix d'un appartement en fonction de sa taille et de son nombre de pièces (encore une fois les données sont fictives):
| Taille (m²) | Nombre de pièces | Prix (millier €) |
|---|---|---|
| 112 | 4 | 253 |
| 203 | 6 | 760 |
| 158 | 5 | 558 |
| 98 | 3 | 243 |
| 143 | 4 | 302 |
Nos matrices ressembleront à ceci :
\[\begin{aligned} x = \begin{bmatrix} 112 & 4 \\ 203 & 6 \\ 158 & 5 \\ 98 & 3 \\ 143 & 4 \end{bmatrix} y = \begin{bmatrix} 253 \\ 760 \\ 558 \\ 243 \\ 302 \end{bmatrix} \end{aligned}\]
Le modèle qu'on cherche à construire est une fonction linéaire, qu'on notera :
\(h_{\theta}(x) = \theta_{0} + \theta_{1}x_1 + \theta_{2}x_2 + \ldots + \theta_{n}x_n\)
\(\theta\) correspond aux coefficients de notre fonction qui prend \(n\) attributs (ou feature en anglais). Les attributs sont les différentes colonnes de \(x\) (la puissance d'un ordinateur, la taille d'un appartement, le nombre de pièces, etc.) et c'est sur quoi se base l'algorithme pour généraliser le problème qu'on lui donne. Il est très important de bien choisir les attributs, et de renseigner uniquement ceux qui ont une réelle influence sur le résultat, mais sans pour autant en donner trop peu à l'algorithme.
On souhaite donc trouver une fonction \(h_{\theta}\), aussi appelée fonction d'hypothèse, tel que \(h(x) \simeq y\). Le problème que cherche à résoudre la régression linéaire est de trouver les paramètres \(\theta\) qui rendent notre modèle proche de la réalité (représentée par \(y\)) afin qu'il soit efficace.
Si l'on reprend notre énoncé de départ sur le prix d'un ordinateur, on a uniquement un attribut (sa puissance), et on cherche une estimation du prix à l'aide d'une fonction d'hypothèse de la forme :
\(h_{\theta}(x) = \theta_{0} + \theta_{1}x_1\)
Mais pour comprendre comment trouver un bon modèle, il faut tout d'abord comprendre comment décrire l'efficacité d'un modèle quelconque, et surtout qu'est-ce qui rend un modèle meilleur qu'un autre ?
Afin de différencier deux modèles en fonction de leurs efficacités, on va utiliser une fonction d'erreur qui mesure le taux d'erreur entre notre modèle et la réalité.
Si on prend un exemple \(i\), la différence entre l'estimation de notre fonction d'hypothèse et la sortie fournie en entrée se note :
\(h_{\theta}(x_{i}) - y_{i}\)
Où \(x_{i}\) et \(y_{i}\) désignent le \(i\)ème exemple sous la forme d'un couple (entrée, sortie). Cependant, cette valeur peut être négative, on va donc la monter au carré car cela nous permet aussi d'amplifier le résultat (s'il y a une grosse différence, alors le carré produira un résultat très élevé et inversement). Si on avait utilisé une autre fonction pour rendre l'expression positive, comme la valeur absolue, on n'aurait pas eu cette deuxième propriété intéressante qui permet de mieux distinguer deux modèles en fonction de leurs efficacités.
\((h_{\theta}(x_{i}) - y_{i})^2\)
Vu qu'il y a \(m\) exemples en entrée, on va faire la moyenne de toutes les différences au carré pour prendre chaque exemple en compte dans notre fonction d'erreur :
\(\frac{1}{m} \displaystyle\sum_{i=1}^{m} (h_{\theta}(x_{i}) - y_{i})^2\)
Si on reprend la généralisation qu'on a faite à la main, la différence que l'on calcule dans notre expression correspond aux parties vertes sur ce schéma :

On notera cette fonction \(J\), qu'on appelle aussi l'**estimateur des moindres carrés** :
\(J(\theta) = \frac{1}{m} \displaystyle\sum_{i=1}^{m} (h_{\theta}(x_{i}) - y_{i})^2\)
Par convention, et pour simplifier nos futurs calculs, on divise le résultat obtenu par 2 :
\(J(\theta) = \frac{1}{2m} \displaystyle\sum_{i=1}^{m} (h_{\theta}(x_{i}) - y_{i})^2\)
Cette fonction d'erreur nous permet alors de comparer deux modèles en fonction des paramètres \(\theta\) qu'ils utilisent. Il est d'ailleurs possible de démontrer que cette fonction est un estimateur optimal sous certaines hypothèses grâce au théorème de Gauss-Markov, c'est pour cela qu'elle est utilisée quasiment dans tous les cas de régression linéaire et polynomiale.
Grâce à cela, on peut enfin définir concrètement ce que signifie "trouver le meilleur modèle". Cela revient à trouver des paramètres \(\theta\) qui minimisent la fonction d'erreur utilisée.
Si l'on affiche graphiquement la fonction d'erreur pour notre problème, on obtient ceci :

Sur ce graphique représentant \(J\) en fonction de \(\theta_{0}\) et \(\theta_{1}\), on remarque clairement les valeurs de \(\theta\) pour lesquelles la fonction d'erreur est minimisée. Cependant, il va falloir trouver un algorithme qui calcule ces valeurs automatiquement, car on ne pourra pas toujours faire de représentation graphique (lorsqu'on a beaucoup d'attributs en entrée par exemple).
On a réussi à définir mathématiquement l'objectif de la régression linéaire grâce à notre fonction d'erreur. Désormais il faut donc minimiser cette fonction avec les paramètres \(\theta\).
Deux méthodes répandues s'offrent à nous :
Maintenant qu'on a vu comment fonctionne la régression linéaire, il est temps d'utiliser des fonctions polynomiales plus complexes afin de généraliser sur des données non linéaires. En réalité, l'unique changement à réaliser est sur notre fonction d'hypothèse puisque la fonction d'erreur et les deux algorithmes restent exactement les mêmes. Il suffit donc d'employer une fonction d'hypothèse polynomiale :
\(h_{\theta}(x) = \theta_{0} + \theta_{1}x_1 + \theta_{2}x_2^2 + \ldots + \theta_{n}x_n^d\)
Dans cette expression, \(d\) correspond au degré maximum de notre fonction.
Dans le cas où on a peu d'attributs, et qu'on veut une fonction très complexe, il est tout à fait possible d'utiliser plusieurs fois les mêmes attributs mais avec différents degrés, par exemple :
\(h_{\theta}(x) = \theta_{0} + \theta_{1}x_1 + \theta_{2}x_1^2 + \theta_{3}x_1^3\)
Il est aussi courant d'ajouter d'autres termes que de simples puissances, comme des exponentiations, des logarithmes, des racines carrées, des fonctions trigonométriques, etc. dans le but de modéliser des fonctions avec un aspect particulier pour bien coller à nos données.
Si possible, afficher les données sur un graphique est la meilleure chose à faire afin de pouvoir visualiser quels types d'attributs il nous faut pour notre fonction d'hypothèse. Sinon, il est toujours envisageable de tester plusieurs combinaisons et de voir laquelle est la meilleure en fonction du résultat de la fonction d'erreur.

Dans le domaine de l'apprentissage artificiel, il y a un problème commun à de très nombreux algorithmes : le surapprentissage.
Dans un apprentissage supervisé, le but est de fournir à notre algorithme des exemples à partir desquels il peut généraliser le problème à résoudre. Cependant, il arrive que ce dernier ne généralise pas assez, et en vient à réciter par cœur les données fournies. Le problème est que notre programme va alors trouver la bonne réponse sur quasiment tous nos exemples, mais dès qu'il verra une nouvelle entrée il répondra totalement à côté. Il n'a pas réussi à généraliser, et il est tombé dans le cas par cas. Cette notion de surapprentissage (ou overfitting en anglais) est essentielle à comprendre car c'est un problème extrêmement récurrent dans le domaine de l'apprentissage artificiel, et spécialement dans le cadre d'un apprentissage supervisé. ` Par exemple, prenons des données imaginaires :
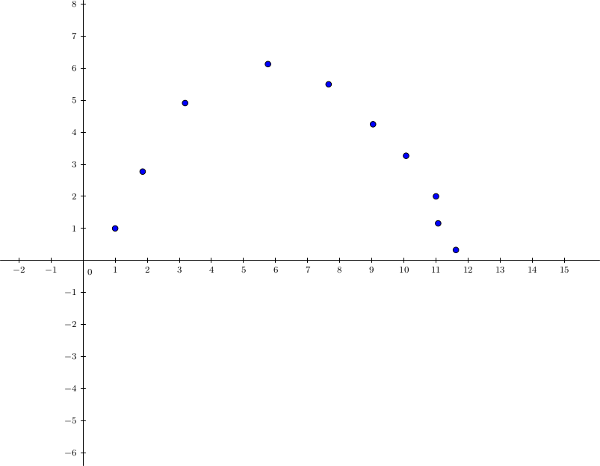
On pourrait tenter d'utiliser une régression linéaire avec une fonction d'hypothèse de la forme \(h_{\theta}(x) = \theta_0 + \theta_1x_1\) :
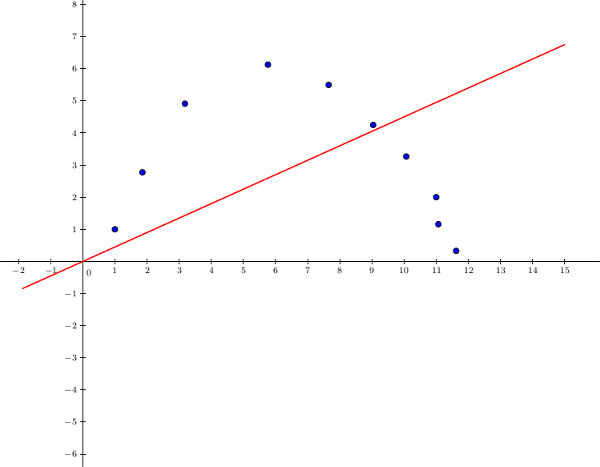
On voit bien qu'on arrive à une très mauvaise généralisation car il nous manque des attributs. Dans ce cas, on parle de sous-apprentissage (ou underfitting en anglais), c'est une situation plus rare que le surapprentissage, et il suffit de rajouter des attributs pour contrer le problème. Essayons, avec une simple fonction polynomiale comme \(h_{\theta}(x) = \theta_0 + \theta_1x_1 + \theta_2x_1^2\) :

Notre modèle polynomial correspond bien à nos données et semble assez bien généraliser le problème. Cependant, que se passe-t-il si on avait rajouté plus d'attributs ? Essayons avec une fonction polynomiale plus complexe comme \(h_{\theta}(x) = \theta_0 + \theta_1x_1 + \theta_2x_1^2 + \theta_3x_1^3 + \theta_4x_1^4 \ldots\) :

Le modèle essaie de coller au mieux à nos données au point de ne plus du tout généraliser le problème, on est tombé dans le surapprentissage. Notre programme s'est trop bien adapté à nos données, et il n'arrivera pas à prédire correctement la sortie de nouveaux exemples.
L'apprentissage supervisé est donc un domaine difficile car il faut arriver à trouver les attributs vraiment nécessaires à notre algorithme pour être le plus efficace possible, sans pour autant tomber dans le surapprentissage. Mais il existe des méthodes afin d'éviter au plus ce problème si contraignant, comme la régularisation.
Le principe de la régularisation est de pénaliser les attributs avec des coefficients ayant des degrés élevés (puisque c'est à cause d'eux que notre modèle a une forme très particulière qui ne généralise pas assez). Si l'on reprend notre dernier exemple avec une fonction d'hypothèse de la forme :
\(h_{\theta}(x) = \theta_0 + \theta_1x_1 + \theta_2x_1^2 + \theta_3x_1^3 + \theta_4x_1^4 \ldots\)
Pénaliser \(\theta_3\) et \(\theta_4\) permettrait d'avoir un modèle qui généralise beaucoup mieux, sans passer par des formes extrêmes.
Pour réaliser cela, il faut ajouter à notre fonction d'erreur un terme de régularisation :
\(J(\theta) = \frac{1}{2m} \left[\displaystyle\sum_{i=1}^{m} (h_{\theta}(x_{i}) - y_{i})^2 + \lambda \displaystyle\sum_{j=1}^{n} \theta_j^2\right]\)
Dans le terme ajouté \(\lambda \displaystyle\sum_{j=1}^{n} \theta_j^2\), on a \(\lambda\) qui correspond au paramètre de la régularisation (et donc qui détermine la puissance de la pénalisation). Il faut aussi noter qu'on ne pénalise pas \(\theta_0\).
Grâce à cela, les coefficients avec des degrés élevés augmenteront fortement le résultat de la fonction d'erreur, obligeant naturellement à nos algorithmes de pénaliser ces derniers. On arrive donc à une fonction d'hypothèse simplifiée, et moins sujet au cas de surapprentissage.
Cependant il faut adapter nos deux algorithmes à cette nouvelle fonction d'erreur, en les modifiant légèrement.
Avec notre ancienne fonction d'erreur, on devait mettre à jour nos coefficients de manière simultanée de cette façon (si l'on n'utilise pas la version vectorisée) :
Pour chaque coefficient \(\theta_j\) avec \(j\) allant de 0 à \(n\) :
\(\theta_{j} = \theta_{j} - \alpha\frac{1}{m}\displaystyle\sum_{i=1}^{m} (h_{\theta}(x_{i}) - y_{i})x_{ij}\)
Désormais, on va avoir :
Pour chaque coefficient \(\theta_j\) avec \(j\) allant de 1 à \(n\) (puisqu'on ne pénalise pas \(\theta_0\), et on utilisera l'ancienne formule pour ce coefficient) :
\(\theta_{j} = \theta_{j} - \alpha\left[\frac{1}{m}\displaystyle\sum_{i=1}^{m} (h_{\theta}(x_{i}) - y_{i})x_{ij} + \frac{\lambda}{m}\theta_j\right]\)
On a obtenu cette formule de la même manière que pour l'ancienne, c'est-à-dire en calculant la dérivée partielle de la fonction d'erreur.
Pour l'équation normale, on applique de nouveau notre démonstration mais sur notre nouvelle fonction d'erreur, ce qui nous donne le résultat suivant :
\(\theta = \left(x^\intercal x + \lambda \left[\begin{smallmatrix} 0\\ &1\\ &&1 \\ &&&\ddots \\ &&&&1 \end{smallmatrix}\right]\right)^{-1} x^\intercal y\)
On retrouve notre paramètre de régularisation \(\lambda\), ainsi qu'une matrice de taille \((n + 1)\times(n + 1)\) assez spéciale composée de 1 uniquement dans la diagonale en partant de la deuxième colonne (le reste de la matrice contient des 0). Cette matrice est en réalité une matrice identité sans le premier terme en haut à gauche (en rapport avec \(\theta_0\) qui n'est pas pénalisé).
Avec un paramètre \(\lambda\) très large, on tombe dans le cas du sous-apprentissage car nos coefficients seront tellement pénalisés qu'on risque d'avoir une fonction d'hypothèse trop simple pour notre problème. À l'inverse, un paramètre \(\lambda\) trop petit ne va pas assez pénaliser les coefficients avec des degrés élevés ce qui n'atténuera pas notre problème de surapprentissage et sera donc inutile.
Il faut alors réussir à choisir un bon paramètre de régularisation \(\lambda\), et pour cela on peut s'aider de différents échantillons, ainsi que de la validation croisée. Jusqu'à présent, le seul échantillon de nos données qu'on utilisait était l'échantillon d'apprentissage. On va désormais rajouter deux nouveaux échantillons :
On n'utilisera pas l'échantillon de test dans le choix du paramètre \(\lambda\), mais il est important d'en parler car en général sur nos données on les divise entre nos différents échantillons de tel sorte à avoir environ 60% des données dans l'échantillon d'apprentissage, 20% dans celui de test, et 20% dans celui de validation.
Le principe de la validation croisée est de tester différentes valeurs de \(\lambda\) et sélectionner la meilleure grâce à notre fonction d'erreur et à nos échantillons :
Notez qu'on peut utiliser cette méthode de validation croisée afin de choisir les degrés à utiliser dans notre fonction d'hypothèse polynomiale de la même façon que pour \(\lambda\).
La régression linéaire et polynomiale est donc un moyen de généraliser un problème à partir d'exemples fournis en construisant un modèle plus ou moins complexe. On a pu voir deux algorithmes très différents, ainsi que le principal problème lié à ce type d'apprentissage avant d'aborder une solution efficace.
Même si l'action de "généraliser" est une notion assez facile à appréhender en tant qu'humain, c'est bien plus compliqué de le faire comprendre à un ordinateur et les mathématiques nous permettent de nous en rapprocher considérablement comme on a pu le voir. L'algorithme du gradient sera d'ailleurs utilisé à travers d'autres algorithmes d'apprentissage artificiel, il était donc important de le découvrir ici dans un cadre assez accessible.
Déduire un modèle à partir de données est un problème très commun, et la régression linéaire et polynomiale est une méthode employée dans pleins de domaines comme l'économie, la finance, les statistiques, la géographie, la physique, la biologie, etc.