Dans le cadre d'une régression linéaire, on cherche à définir une fonction d'hypothèse proche de la réalité et de la forme :
\(h_{\theta}(x) = \theta_{0} + \theta_{1}x_1 + \theta_{2}x_2 + \ldots + \theta_{n}x_n\)
Par convention et pour simplifier le code, il n'est pas rare de rajouter un attribut \(x_0 = 1\), afin de remplacer notre fonction par :
\(h_{\theta}(x) = \displaystyle\sum_{i=0}^{n} \theta_{i}x_{i}\)
Cependant, \(\theta\) et \(x\) sont deux matrices, et le calcul de la fonction d'hypothèse pourrait s'écrire sous la forme d'un simple produit matriciel :
\(h_{\theta}(x) = \theta^\intercal x = x \theta\)
Notre but est de chercher une fonction d'hypothèse efficace, et ceci revient à trouver les coefficients \(\theta\) de \(h_{\theta}\) qui minimisent la fonction d'erreur \(J\). Pour rappel, notre fonction d'erreur ressemble à cela :
\(J(\theta) = \frac{1}{2m} \displaystyle\sum_{i=1}^{m} (h_{\theta}(x_{i}) - y_{i})^2\)
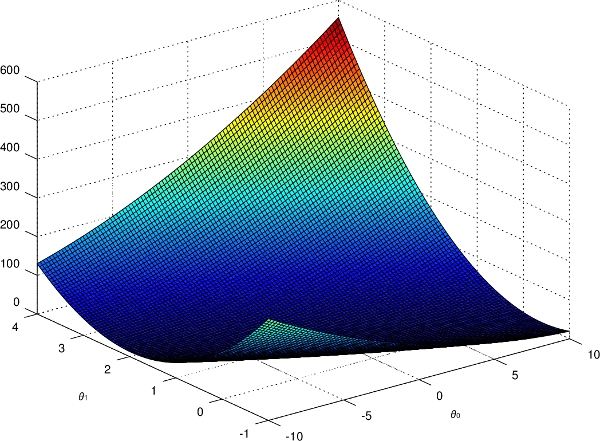
Et si on reprend l'exemple du prix de l'ordinateur, et qu'on affiche \(J\) en fonction de \(\theta_0\) et \(\theta_1\), on obtenait ce graphique en trois dimensions :

On va donc appliquer notre algorithme du gradient (gradient descent en anglais) afin de résoudre notre problème de minimisation.
L'idée de l'algorithme est de commencer avec des paramètres initiaux \(\theta\) (en général on utilise 0), puis d'adapter ces derniers avec le résultat obtenu par notre fonction d'erreur, afin de minimiser \(J\) et arriver à un minimum local. Il est possible que ce minimum local, soit le minimum global de notre fonction d'erreur, mais l'algorithme ne le garantit pas car le résultat dépendra de l'initialisation des coefficients \(\theta\).
Il est plus difficile de visualiser l'idée de l'algorithme sur notre précédent graphique en 3D, alors on va utiliser un graphique 2D spécial qui trace les contours (on appelle cela un contour plot en anglais) :
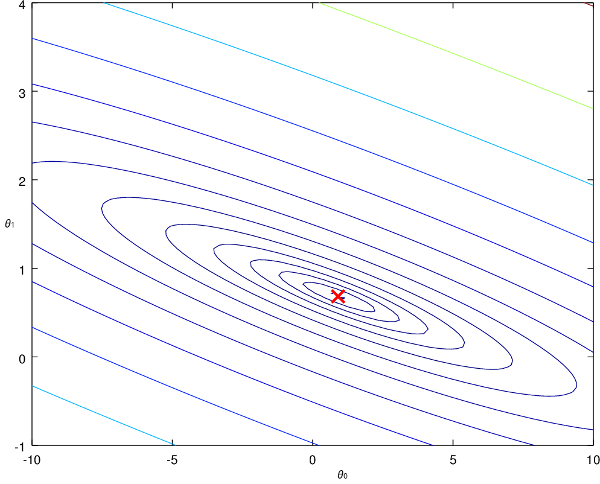
Les contours représentent \(J\) en fonction de nos deux coefficients \(\theta_{0}\) et \(\theta_{1}\). La croix rouge correspond au minimum de la fonction d'erreur, et c'est le point qu'on cherche à atteindre.
L'algorithme du gradient va procéder ainsi :
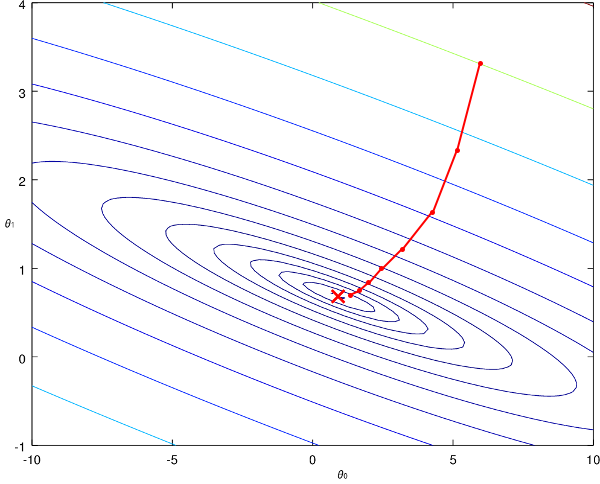
On part d'un point initial sur le graphique, et on fait des pas de plus en plus petits afin de se rapprocher du minimum de la fonction. Cependant, comment l'algorithme réalise-t-il ces pas ? Comment est-ce qu'il décide de l'amplitude, ou encore de la direction à emprunter ?
Pour comprendre l'algorithme, on peut imaginer que ce dernier utilise la "pente" de la représentation de la fonction pour décider du prochain point à explorer. Par exemple sur notre graphique en 3D, il suffit d'imaginer une boule qu'on place sur la figure et qui va rouler jusqu'à arriver dans un creux ou une surface assez plane. Mathématiquement parlant, la décision du prochain point à parcourir se fera grâce à la dérivée partielle de la fonction \(J\) au point actuel de notre algorithme.
Simplifions notre problème avec un exemple de fonction \(J\) prenant uniquement un paramètre \(\theta_{0}\) :
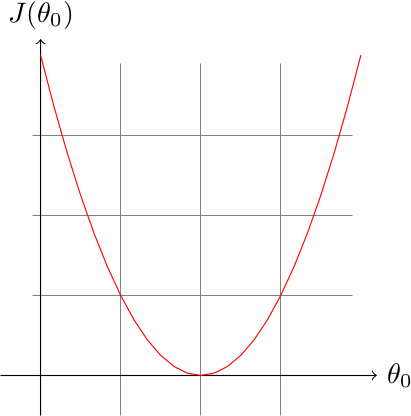
On initialise l'algorithme avec un point tel que \(\theta_{0} = 0\), et on calcule la dérivée partielle de la fonction \(J\) en ce point :
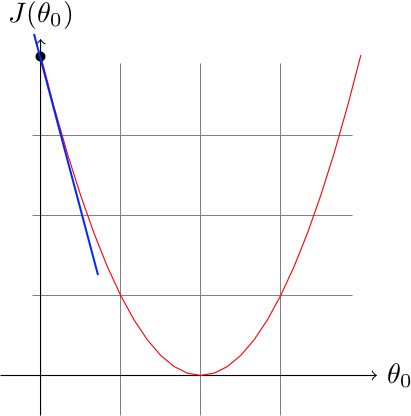
La dérivée partielle est la droite en bleue, et on remarque que le coefficient directeur de la tangente est négatif et important, notre algorithme va donc augmenter \(\theta_{0}\) de manière importante.
On peut continuer ainsi jusqu'à tomber sur le minimum de notre fonction :
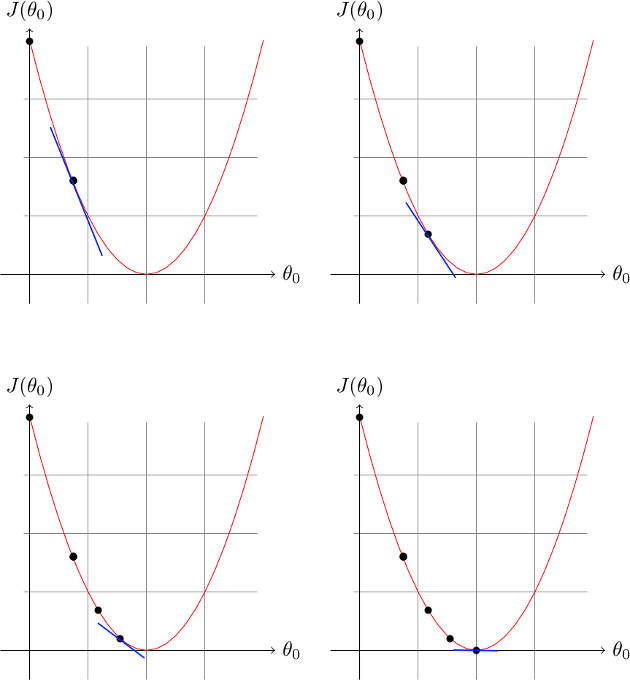
Même si on a vu que notre algorithme ne trouvera pas toujours le minimum global de la fonction, un minimum local est toujours intéressant, et sur des problèmes très complexes cela sera beaucoup plus efficace à utiliser qu'une approximation faite à la main.
Maintenant qu'on a vu le principe, il faut le décrire de manière concrète et mathématique.
Tant que l'algorithme ne converge pas, on met à jour tous nos coefficients \(\theta\) pour \(j\) allant de 0 à \(n\) :
\(\theta_{j} = \theta_{j} - \alpha\frac{\partial}{\partial\theta_{j}}J(\theta)\)
\(\alpha\) est notre vitesse d'apprentissage qui sert à réguler la rapidité de la convergence. La dérivée partielle de \(J\) est représentée par \(\frac{\partial}{\partial\theta_{j}}J(\theta)\), et lorsqu'on calcule cette dérivée on obtient l'expression suivante :
\(\frac{\partial}{\partial\theta_{j}}J(\theta) = \frac{1}{m}\displaystyle\sum_{i=1}^{m} (h_{\theta}(x_{i}) - y_{i})x_{ij}\)
Notre formule développée est donc :
\(\theta_{j} = \theta_{j} - \alpha\frac{1}{m}\displaystyle\sum_{i=1}^{m} (h_{\theta}(x_{i}) - y_{i})x_{ij}\)
Dans notre détail de l'algorithme du gradient, il y a un point très important à ne pas négliger : la mise à jour de manière instantanée. Vu que notre expression dépend elle-même de \(\theta\), on ne peut pas se permettre de modifier certaines valeurs lorsqu'on met à jour nos coefficients un à un, il faut donc procéder en deux étapes bien distinctes :
Si l'on garde notre exemple avec un attribut, on aurait ces opérations à effectuer :
\(temp0 = \theta_{0} - \alpha\frac{1}{m}\displaystyle\sum_{i=1}^{m} (h_{\theta}(x_{i}) - y_{i})x_{i0}\)
\(temp1 = \theta_{1} - \alpha\frac{1}{m}\displaystyle\sum_{i=1}^{m} (h_{\theta}(x_{i}) - y_{i})x_{i1}\)
\(\theta_{0} = temp0\)
\(\theta_{1} = temp1\)
Le pseudo-code définitif ressemble donc à ceci :
Initialiser tous les coefficients à 0
Tant qu'on n'a pas dépassé la limite de tours
Pour chaque coefficient
Calculer temp[j]
Pour chaque coefficient
theta[j] = temp[j]Notre boucle principale n'utilise plus la condition de convergence de notre algorithme du gradient pour plusieurs raisons :
Il est primordial de bien choisir le coefficient d'apprentissage, car si \(\alpha\) est trop élevé notre algorithme va chercher à faire de très grands pas afin de converger rapidement (en anglais on utilise le terme d'*overshoot*), et ceci peut l'amener à faire de mauvais choix comme :
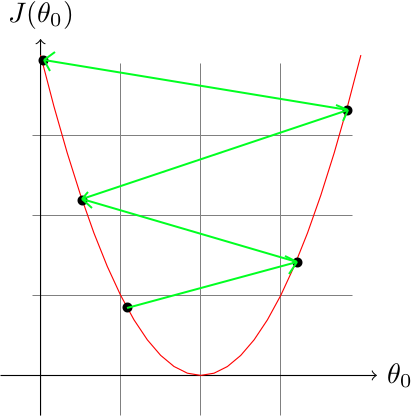
L'algorithme risque alors de ne pas converger, voire de diverger.
À l'inverse, une vitesse d'apprentissage trop faible rendra notre algorithme terriblement lent :
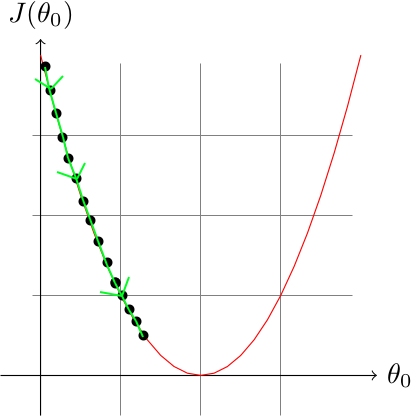
Pour choisir une valeur adaptée à notre problème, il faut en essayer différentes (0.001, 0.01, 0.1, 1, 10, etc.) tout en créant un graphique représentant l'évolution de notre minimisation de \(J\) en fonction du nombre d'itérations de l'algorithme. Si vous avez bien choisi le coefficient, vous devriez voir un graphique semblable à ceci :
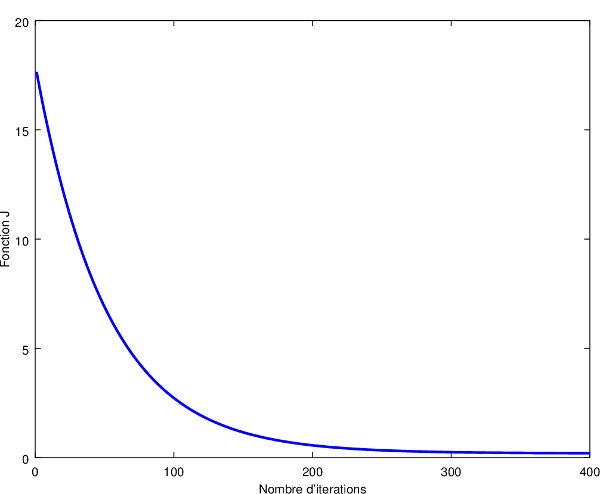
On remarque bien que notre algorithme minimise bien la fonction d'erreur au fur et à mesure qu'il itère, ce qui signifie que notre vitesse d'apprentissage est adaptée à notre problème.
Voici le code en Python pour l'algorithme du gradient :
J'utilise Python afin d'avoir accès à des librairies scientifiques comme `numpy <http://www.numpy.org/>`__ pour les matrices et `matplotlib <http://matplotlib.org/>`__ pour les graphiques.
import numpy as np
# x = exemple d'entrée
# y = exemple de sortie
# m = nombre d'exemples
# n = nombre d'attributs
# theta = coefficients de notre fonction d'hypothese
class regression_lineaire:
def __init__(self, entree):
with open(entree) as f:
self.m, self.n = map(int, f.readline().split())
self.x = np.matrix(np.loadtxt(entree, skiprows=1,
usecols=(list(range(self.n))), ndmin=2))
self.y = np.matrix(np.loadtxt(entree, skiprows=1,
usecols=([self.n]), ndmin=2))
# Ajoute une colonne de 1 au début de notre matrice x
col = np.ones((self.m, 1))
self.x = np.matrix(np.hstack((col, self.x)))
self.n = self.n + 1
def algo_gradient(self, alpha, nb_tour_max):
# Initialise à 0 les coefficients de la fonction d'hypothese
self.theta = np.matrix(np.zeros((self.n, 1)))
for _ in range(nb_tour_max):
# Pour faire la mise à jour instantanée des coefficients :
# 1. On calcule d'abord les résultats dans des variables temporaires
temp = np.zeros((self.n, 1))
for j in range(self.n):
somme = 0.0
for i in range(self.m):
hypothese = float(self.x[i] * self.theta)
somme = somme + ((hypothese - self.y[i]) * self.x.item((i, j)))
temp[j] = self.theta[j] - alpha * (1 / self.m) * somme
# 2. Puis on copie les résultats dans nos coefficients
for j in range(self.n):
self.theta[j] = temp[j]
ia = regression_lineaire("test01.in")
ia.algo_gradient(0.01, 400)
print("Coefficients de la fonction d'hypothese :\n")
for j in range(ia.n):
print("theta ", j, " : ", float(ia.theta[j]))Notre fichier d'entrée contient sur la première ligne le nombre \(m\) d'exemples, puis le nombre \(n\) d'attributs. Sur les \(m\) prochaines lignes, on retrouve une liste de nombre dont la dernière colonne correspond à \(y\) et les autres à \(x\). J'ai repris notre exemple de l'introduction pour construire le fichier d'entrée (les unités sont toujours en centaine d'opérations et en centaine d'euros) :
6 1
1.73 1.94
4.07 2.87
5.34 5.01
7.14 6.74
9.56 7.71
12.26 8.6En sortie on obtient les coefficients \(\theta\) de notre fonction d'hypothèse :
Coefficients de la fonction d'hypothese :
theta 0 : 0.5764647547614207
theta 1 : 0.7219164912370313Vu qu'on a uniquement un attribut (la puissance d'un ordinateur), on peut représenter notre fonction d'hypothèse et nos données en entrée sur un graphique 2D :
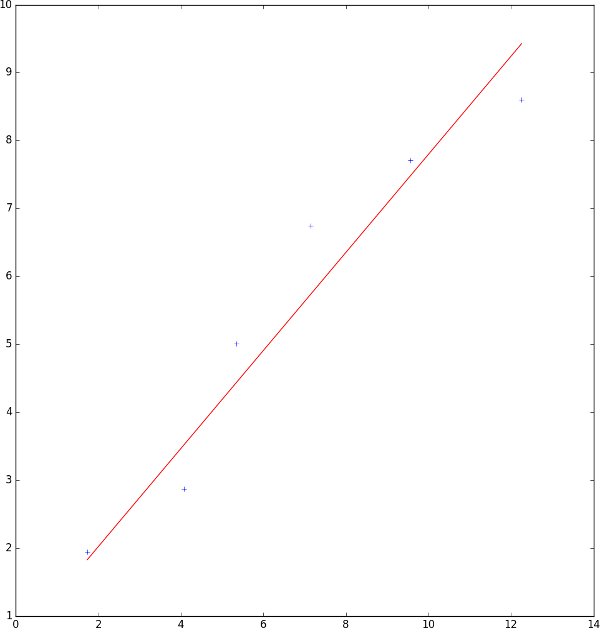
On obtient bien une généralisation efficace sous forme de fonction linéaire qui ressemble fortement à celle qu'un humain peut faire à la main (même si celle que l'ordinateur a calculé est plus précise que celle faite à la main).
Le code utilisé pour réaliser cette sortie :
import matplotlib.pyplot as plt
# Récupère dans des listes les valeurs de x, y, et de notre approximation de y
x = np.array(ia.x[:,1]).tolist()
x = [float(i[0]) for i in x]
y = np.array(ia.y).tolist()
y = [float(i[0]) for i in y]
y_approx = np.array(ia.x * ia.theta).tolist()
y_approx = [float(i[0]) for i in y_approx]
# Affiche les points donnés en entrée, ainsi que notre modèle linéaire
plt.plot(x, y, '+')
plt.plot(x, y_approx, 'r-')
plt.show()Afin de simplifier le code, il serait utile d'utiliser la même amélioration qu'avec notre fonction d'hypothèse : les opérations sur les matrices. Au lieu d'appliquer des opérations sur les éléments d'une matrice un par un, on peut utiliser des opérations plus générales sur notre matrice entière. Cela permet de supprimer la plupart des boucles, mais aussi, a le gros avantage de réaliser une mise à jour instantanée des coefficients automatiquement, sans même avoir besoin de stocker nos résultats dans des variables temporaires. On peut donc transformer notre algorithme du gradient en ceci :
\(\theta = \theta - \alpha\frac{1}{m}x^\intercal(h_{\theta}(x) - y)\)
Si on développe notre fonction d'hypothèse on arrive à cette expression :
\(\theta = \theta - \alpha\frac{1}{m}x^\intercal(x\theta - y)\)
Il n'y a plus aucunes boucles, et uniquement des opérations matricielles. Notre fonction pour l'algorithme du gradient devient donc dans notre code :
def algo_gradient(self, alpha, nb_tour_max):
# Initialise à 0 les coefficients de la fonction d'hypothese
self.theta = np.matrix(np.zeros((self.n, 1)))
for _ in range(nb_tour_max):
derivee = np.transpose(self.x) * (self.x * self.theta - self.y)
self.theta = self.theta - alpha * (1 / self.m) * deriveeLe code est beaucoup plus concis de cette manière, ce qui rend sa lecture plus facile et agréable.
Dans le cas de généralisation d'un problème avec plusieurs attributs, il est possible que l'échelle de valeurs possibles soit très différente d'un attribut à un autre. Par exemple, dans l'estimation du prix d'un ordinateur, le nombre d'opérations que l'ordinateur effectue à la seconde représente un nombre bien plus important que le nombre de ventilateurs à l'intérieur de la machine. Si on affiche un contour plot dans cette situation, on verrait ce phénomène :
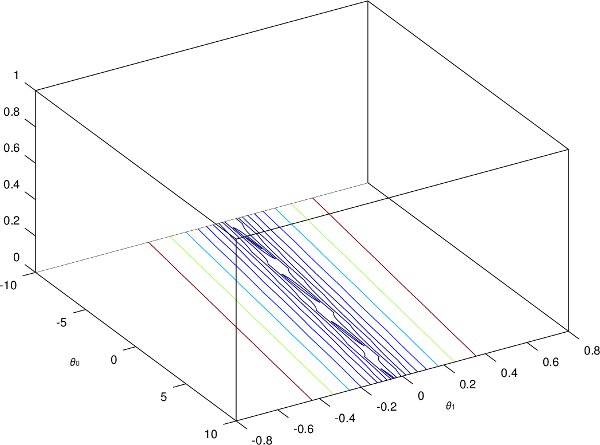
Le problème ici est que notre algorithme du gradient va mettre beaucoup plus de temps à converger vers un minimum, car on a de longs et fins contours. À l'inverse, si on arrive à rendre les échelles similaires, on aurait plutôt un graphique qui ressemble à cela :
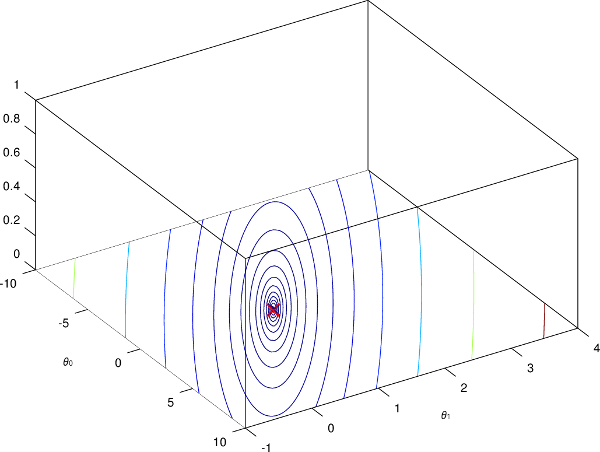
Notre algorithme va alors converger bien plus rapidement.
Pour réaliser cette opération dite de feature scaling en anglais, on utilise une méthode de standardisation (aussi appelée mean normalization dans notre cas). Le but est d'avoir toutes nos valeurs de \(x\), tel qu'on a approximativement \(-1 \leq x \leq 1\). On va donc modifier chaque valeur \(i\) de \(x\) :
\(x_i = \frac{x_i - \bar{x_i}}{\sigma_i}\)
\(\bar{x}\) représente la moyenne, et \(\sigma\) est l'écart type (qui nous sert à mesurer la dispersion de nos valeurs).
Il faut en revanche faire attention à ne pas appliquer cela sur \(x_0\) car cette valeur doit toujours être égale à 1, on réalisera donc l'opération de feature scaling avant d'ajouter notre colonne de 1 à \(x\) :
# Feature scaling
self.x = (self.x - np.mean(self.x)) / np.std(self.x)Notre sortie n'est alors plus la même puisque nos valeurs ont été changées pour être sur une échelle similaire :
Coefficients de la fonction d'hypothese :
theta 0 : 5.379994218974877
theta 1 : 2.3208884389927897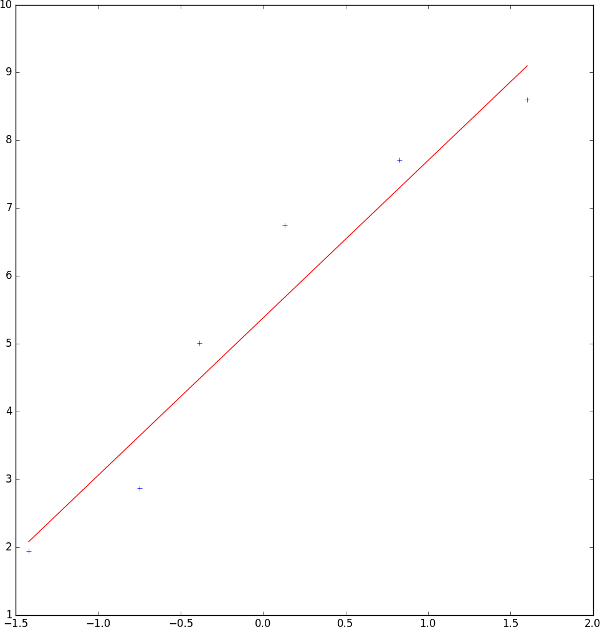
Le code final avec les deux améliorations :
import numpy as np
# x = exemple d'entrée
# y = exemple de sortie
# m = nombre d'exemples
# n = nombre d'attributs
# theta = coefficients de notre fonction d'hypothese
class regression_lineaire:
def __init__(self, entree):
with open(entree) as f:
self.m, self.n = map(int, f.readline().split())
self.x = np.matrix(np.loadtxt(entree, skiprows=1,
usecols=(list(range(self.n))), ndmin=2))
self.y = np.matrix(np.loadtxt(entree, skiprows=1,
usecols=([self.n]), ndmin=2))
# Feature scaling
self.x = (self.x - np.mean(self.x)) / np.std(self.x)
# Ajoute une colonne de 1 au début de notre matrice x
col = np.ones((self.m, 1))
self.x = np.matrix(np.hstack((col, self.x)))
self.n = self.n + 1
def algo_gradient(self, alpha, nb_tour_max):
# Initialise à 0 les coefficients de la fonction d'hypothese
self.theta = np.matrix(np.zeros((self.n, 1)))
for _ in range(nb_tour_max):
derivee = np.transpose(self.x) * (self.x * self.theta - self.y)
self.theta = self.theta - alpha * (1 / self.m) * derivee
ia = regression_lineaire("test01.in")
ia.algo_gradient(0.01, 400)
print("Coefficients de la fonction d'hypothese :\n")
for j in range(ia.n):
print("theta ", j, " : ", float(ia.theta[j]))L'algorithme du gradient est donc un algorithme itératif servant à minimiser notre fonction d'erreur \(J\) afin de trouver les paramètres \(\theta\) optimaux pour notre fonction d'hypothèse. Cet algorithme est très utile sur des entrées extrêmement importantes car on peut contrôler son nombre d'itérations ainsi que sa vitesse d'apprentissage (qu'il faut bien choisir au risque de réduire considérablement l'efficacité de notre programme).
Il faut savoir qu'il existe différentes variantes de cet algorithme :