Contrairement à l'algorithme du gradient l'équation normale est une expression mathématique et non pas un algorithme itératif, qui permet de résoudre notre problème de régression linéaire en trouvant les valeurs de \(\theta\) pour lesquelles notre fonction \(J\) est minimisée.
L'équation normale est définie comme ceci :
\(\theta = (x^\intercal x)^{-1} x^\intercal y\)
On peut grâce à cela calculer directement \(\theta\) qui permet d'obtenir notre fonction d'hypothèse tel que \(h_{\theta} \simeq y\).
Reprenons notre fonction d'hypothèse :
\(h_{\theta} = x\theta\)
Ainsi que notre fonction d'erreur :
\(J(\theta) = \frac{1}{2m} \displaystyle\sum_{i=1}^{m} (h_{\theta}(x_{i}) - y_{i})^2\)
Vu que \(x\) et \(\theta\) sont deux matrices, on peut se permettre de réécrire notre fonction \(J\) en utilisant des opérations matricielles et en remplaçant la fonction d'hypothèse par son contenu :
\(J(\theta) = \frac{1}{2m} (x\theta - y)^\intercal (x\theta - y)\)
Or, soit \(A\) et \(B\) deux matrices on a \((A + B)^\intercal = A^\intercal + B^\intercal\), donc :
\(J(\theta) = \frac{1}{2m} ((x\theta)^\intercal - y^\intercal)(x\theta - y)\)
Plus loin dans la démonstration on va dériver cette fonction puis la comparer à 0, le facteur \(\frac{1}{2m}\) sera donc inutile et il n'y a pas besoin de le garder ici :
\(J(\theta) = ((x\theta)^\intercal - y^\intercal)(x\theta - y)\)
Développons les deux facteurs :
\(J(\theta) = (x\theta)^\intercal x\theta - (x\theta)^\intercal y - y^\intercal (x\theta) + y^\intercal y\)
On sait que \(y\) est un vecteur et que le résultat de la multiplication matricielle \(x\theta\) l'est aussi, l'ordre de multiplication des deux ne change donc rien et on peut simplifier \(- (x\theta)^\intercal y - y^\intercal (x\theta)\) en \(-2(x\theta)^\intercal y\) :
\(J(\theta) = (x\theta)^\intercal x\theta -2(x\theta)^\intercal y + y^\intercal y\)
On peut continuer de développer notre expression puisque \((AB)^\intercal = B^\intercal A^\intercal\) :
\(J(\theta) = \theta^\intercal x^\intercal x\theta - 2(x\theta)^\intercal y + y^\intercal y\)
Pour trouver \(\theta\) à partir de cette expression, il faut dériver la fonction \(J\) et comparer le résultat à 0. On obtient :
\(\frac{\partial J}{\partial\theta} = 2x^\intercal x\theta - 2x^\intercal y\)
\(2x^\intercal x\theta - 2x^\intercal y = 0\)
On ajoute \(2x^\intercal y\) de chaque côté de l'équation, et on divise par deux l'expression :
\(x^\intercal x\theta = x^\intercal y\)
Si la matrice résultant du calcul de \(x^\intercal x\) est inversible, alors on peut multiplier les deux côtés par l'inverse de cette dernière et ainsi affirmer que :
\(\theta = (x^\intercal x)^{-1} x^\intercal y\)
On retrouve bien notre équation normale.
La raison pour laquelle cette méthode n'est pas tout le temps utilisée est assez simple : la rapidité.
En effet, le produit matriciel est encore un problème ouvert car on ne sait pas s'il existe de meilleurs algorithmes que ceux employés aujourd'hui. L'algorithme naïf de multiplication matriciel a une complexité en temps de \(O(N^3)\) avec \(N\) le nombre de lignes des matrices, cependant, les autres algorithmes n'ont pas une complexité si différente (\(O(N^{2.807})\) pour l'algorithme de Strassen ou encore \(O(N^{2.376})\) pour l'algorithme de Coppersmith-Winograd).
Il est donc peu envisageable d'implémenter la méthode de l'équation normale lorsqu'on a environ \(n > 10000\).
Le code en Python permettant de calculer les paramètres \(\theta\) avec l'équation normale :
import numpy as np
# x = exemple d'entrée
# y = exemple de sortie
# m = nombre d'exemples
# n = nombre d'attributs
# theta = coefficients de notre fonction d'hypothese
class regression_lineaire:
def __init__(self, entree):
with open(entree) as f:
self.m, self.n = map(int, f.readline().split())
self.x = np.matrix(np.loadtxt(entree, skiprows=1,
usecols=(list(range(self.n))), ndmin=2))
self.y = np.matrix(np.loadtxt(entree, skiprows=1,
usecols=([self.n]), ndmin=2))
# Ajoute une colonne de 1 au début de notre matrice x
col = np.ones((self.m, 1))
self.x = np.matrix(np.hstack((col, self.x)))
self.n = self.n + 1
def equation_normale(self):
x_t = np.transpose(self.x)
self.theta = (x_t * self.x).I * x_t * self.y
ia = regression_lineaire("test01.in")
ia.equation_normale()
print("Coefficients de la fonction d'hypothese :\n")
for j in range(ia.n):
print("theta ", j, " : ", float(ia.theta[j]))Afin d'optimiser légèrement le programme, la matrice transposée de \(x\) est stockée dans une variable car on doit la calculer deux fois (il est donc parfaitement inutile de refaire la même opération, même si ce n'est pas l'une des plus couteuses).
En entrée de notre programme, on donne le même fichier que pour l'algorithme du gradient :
6 1
1.73 1.94
4.07 2.87
5.34 5.01
7.14 6.74
9.56 7.71
12.26 8.6En sortie en revanche, on obtient des paramètres \(\theta\) différents car l'initialisation de \(\theta\), le coefficient d'apprentissage, le nombre d'itérations maximum et l'opération de feature scaling influent sur le résultat :
Coefficients de la fonction d'hypothese :
theta 0 : 0.9424111325332967
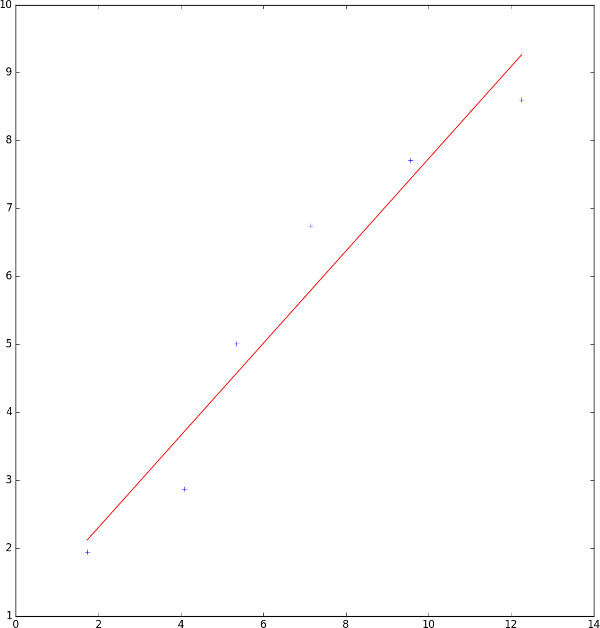
theta 1 : 0.678691601117212Et voici la représentation graphique de notre fonction d'hypothèse trouvée (le code utilisé est le même que celui pour l'algorithme du gradient) :

La méthode de l'équation normale est donc plus précise que celle de l'algorithme du gradient car elle calcule le minimum global de la fonction d'erreur en déterminant \(\theta\) directement avec une relation mathématique. Cependant, on ne peut pas employer cette équation tout le temps car elle a une complexité en temps trop élevée, ce qui la rend quasiment inutilisable sur des entrées où \(n > 10000\).