Tri par base

Introduction

Le tri par base (radix sort en anglais) est un algorithme de tri ayant une complexité en temps linéaire, qui fut inventé à l'époque des trieuses de cartes perforées, mais il est encore utilisé de nos jours dans les ordinateurs modernes. Cet algorithme nécessite un autre algorithme de tri pour fonctionner, et ce dernier doit obligatoirement être stable.

Principe de l’algorithme

L’algorithme est simple, on va trier successivement (à l’aide d’un algorithme de tri stable) tous les chiffres des nombres donnés en entrée en commençant par le chiffre le moins significatif jusqu'au plus significatif.

C’est-à-dire que pour des nombres entiers, on va trier tout d’abord les nombres en fonction du chiffre de l’unité, puis trier de nouveau en fonction du chiffre des dizaines, et ainsi de suite jusqu’à atteindre le nombre maximum de chiffre contenu dans un nombre.

Il est important de noter que l’ordre de tri est défini dans l’algorithme de tri utilisé et non dans le tri par base en lui-même.

Exemple

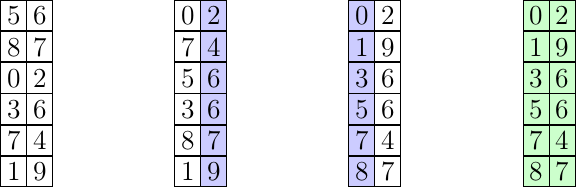
Soit le tableau suivant que l’on souhaite trier dans l’ordre croissant en utilisant l’algorithme du tri par base : 56, 87, 2, 36, 74, 19.

Tout d’abord, on remarque qu’il y a au maximum deux chiffres par nombre et que par conséquent on utilisera notre algorithme de tri stable seulement deux fois. On commence donc par trier cette suite de nombre en fonction du chiffre des unités, puis on recommence l'opération sur le chiffre des dizaines :

On atteint le nombre maximum de chiffre, notre tableau est donc trié :

2, 19, 36, 56, 74, 87.

J'ai découpé les chiffres des nombres pour bien voir le tri de chacun, en bleu on retrouve nos étapes intermédiaires consistantes à trier en fonction d'un chiffre en particulier, et en vert notre tableau final trié.

Pseudo-code

Le pseudo-code du tri par base :

triBase :

   Pour chaque chiffre possible
      Trier Tableau en fonction du chiffre i

Cela peut paraitre assez étrange d'utiliser un autre algorithme de tri dans un algorithme de tri, mais si on se sert du tri par dénombrement on peut ainsi contrer plusieurs de ses défauts tout en gardant sa rapidité d'exécution. Tout d'abord, l'espace mémoire utilisé est bien plus optimisé car on évite les "trous" dans le tableau des effectifs, et ensuite on peut désormais trier des nombres décimaux puisque chaque chiffre reste un nombre entier qu'on peut employer avec le tri par dénombrement.

Complexité

La complexité de ce tri dépend forcément de l'algorithme de tri utilisé dans notre boucle principale, mais supposons qu'on utilise, comme précédemment évoqué, le tri par dénombrement. Pour rappel, ce tri a une complexité en \(O(N + M)\) avec \(N\) la taille du tableau, et \(M\) l'élément maximum du tableau à trier. Soit \(C\) le nombre de chiffres maximum d'un nombre du tableau, on a donc une complexité en temps pour notre algorithme de tri par base en \(O(C(N + M))\), cependant comme notre tri par dénombrement sera uniquement utilisé sur des chiffres, ces derniers ne dépasseront jamais 9 (si on utilise une notation décimale bien sûr), et \(M\) devient alors une constante insignifiante dans le calcul de la complexité, que l'on peut alors simplifier en \(O(CN)\).

Implémentation

Pour implémenter le tri par base, il va tout d'abord falloir modifier légèrement notre implémentation du tri par dénombrement car la notion de stabilité pour ce tri n'a pas vraiment de sens puisqu'on utilise des effectifs sans lien réel avec notre tableau.

Voici une implémentation en C++ du tri par base :

tri_base.cpp

#include <cstdio>
#include <cmath>
#include <queue>
using namespace std;

const int TAILLE_MAX = 1000;

int tableau[TAILLE_MAX];
int taille;

int nbChiffreMax(void)
{
   int max;
   int iTab;

   max = tableau[0];
   for(iTab = 1; iTab < taille; ++iTab)
      if(tableau[iTab] > max)
         max = tableau[iTab];

   return floor(log10(max)) + 1;
}

void trier(int iExp)
{
   queue <int> effectif[10];
   int iTab, iChiffre, iFile;
   int chiffre;
   int nbFile;

   for(iTab = 0; iTab < taille; ++iTab) {
      chiffre = (tableau[iTab] / iExp) % 10;
      effectif[chiffre].push(tableau[iTab]);
   }

   iTab = 0;
   for(iChiffre = 0; iChiffre < 10; ++iChiffre) {
      nbFile = effectif[iChiffre].size();
      for(iFile = 0; iFile < nbFile; ++iFile) {
         tableau[iTab] = effectif[iChiffre].front(); 
         effectif[iChiffre].pop();
         ++iTab;
      }
   }
}

void triBase(void)
{
   int nbChiffre;
   int iChiffre, iExp;

   nbChiffre = nbChiffreMax();
   for(iChiffre = 0, iExp = 1; iChiffre < nbChiffre; ++iChiffre, iExp *= 10)
      trier(iExp);
}

int main(void)
{
   int iTab;

   scanf("%d\n", &taille);

   for(iTab = 0; iTab < taille; ++iTab)
      scanf("%d ", &tableau[iTab]);

   triBase();

   for(iTab = 0; iTab < taille; ++iTab)
      printf("%d ", tableau[iTab]);
   printf("\n");

   return 0;
}

Le code est en C++ afin d'avoir une implémentation facile d'une file car nous en aurons besoin pour modifier notre algorithme de tri par dénombrement. Plusieurs remarques sur ce code :

• Pour trouver le maximum de chiffre d'un nombre du tableau, on cherche l'élément maximum puis on utilise un logarithme de base 10 (que l'on arrondit) afin d'avoir son nombre de chiffres.
• Pour avoir le ième chiffre d'un nombre entier, on le divise par iExp (qui représente \(10^i\) et prend donc les valeurs : 1, 10, 100, etc.) et on applique un modulo 10 dessus (dans le cas où iExp est égal à 1).
• Là où notre algorithme diffère du tri par dénombrement est qu'on veut le rendre stable, or on a vu que la stabilité n'est pas une notion du tri par dénombrement, on utilise donc un tableau de dix files (car on a dix possibilités de chiffre allant de 0 à 9), dans lequel on va ranger les nombres du tableau en fonction du chiffre que l'on étudie. Par exemple, si l'on se trouve dans le premier tour de boucle de notre fonction triBase, on veut alors trier le tableau en fonction du chiffre des unités des nombres, on va donc ranger tous les nombres avec comme chiffre des unités 0 dans la file du tableau à l'indice 0, tous les nombres avec comme unité 1 dans la file du tableau à l'indice 1, etc. Le fait qu'on utilise une file nous permet d'ajouter une stabilité au tri car si un élément se trouve avant un autre dans le tableau, le principe même de la file garanti que cet élément se trouvera avant lui dans la file, et qu'on y accédera avant. Ensuite pour trier à partir de ce tableau de files, on a juste à parcourir tous les chiffres et à défiler les éléments de chaque file pour s'assurer d'avoir un tableau trié en fonction du chiffre demandé grâce à un tri stable en un temps linéaire. Une représentation du tableau de files avec notre exemple du début lors du tri par unité :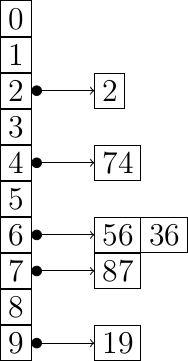

L'entrée de notre exemple :

6
56 87 2 36 74 19

En sortie le tableau trié :

2 19 36 56 74 87

Conclusion

Le tri par base est donc un algorithme de tri très rapide qui s'exécute en temps linéaire en se basant sur un autre algorithme de tri stable pour fonctionner. Il permet notamment de combler les avantages du tri par dénombrement, cependant ce n'est pas pour cela que ce dernier est bien plus efficace que d'autres algorithmes de tri en \(O(N \log _2 N)\) comme le tri rapide et ceci pour plusieurs raisons :

• Le tri par base exécute au maximum \(C\) passes sur le tableau, ce qui est en général moins que pour le tri rapide, mais ces dernières seront plus longues à effectuer, rendant dans certains cas le tri rapide plus efficace que le tri par base, même s'ils ont une complexité en temps différente.
• Les implémentations des deux algorithmes peuvent provoquer de gros changements sur les performances, mais leurs fonctionnements aussi car en général le tri rapide utilisera mieux la mémoire cache que le tri par base ce qui le rend plus utile dans certains cas.
• Notre algorithme implémenté ici avec la version du tri par dénombrement ne trie pas en place les éléments du tableau, et ceci peut poser des problèmes en termes de complexité en mémoire dans certains cas que ne posent pas le tri rapide par exemple.

Encore une fois, le choix d'un algorithme de tri par rapport à un autre dépend de multiples facteurs qu'il faut prendre en compte, d'autant plus que l'entrée peut aussi jouer un grand rôle dans ce choix. Le tri par base reste tout de même utile grâce à sa complexité en temps linéaire efficace.