Paolo Boldi, Sebastiano Vigna (2004): http://www.web.ethz.ch/CDstore/www2004/docs/1p595.pdf
WebGraph Framework: http://webgraph.di.unimi.it/
Features of the links of a web graph:
The final WebGraph compression format uses a mix of methods above.
Reference chains: to access random contents of the graph, we need to decompress all the information from the compression format and follow reference links. This might slow down the access process (worst-case: decompress all the info) so we need to put a limit on the lengths of the reference chains.
We also need to store an offset array of size $N$ if we want to access the graph in random order instead of sequentially.
Lazy iterator: the data is filtered as you request it (it doesn't go through all the list immediately).
Paolo Boldi, Marco Rosa, Massimo Santini (2011): https://arxiv.org/abs/1011.5425
Most compression algorithms exploit properties such as similarity, locality, etc. hence the way nodes are ordered influence a lot the result.
Goal: find a node numbering $\pi$ minimising $P_A(G, \pi)$.
Such optimization problem is NP-Hard, meaning we can only expect heuristics.
Empirical insight: it is important for high compression ratio to use an ordering of vertex IDs such that the vertices from the same host are close to one another.
Note: coordinate-free algorithm means it achieves almost the same compression performance starting from any initial ordering.
The algorithm executes in rounds, every node has a label corresponding to the cluster it belongs to (at the beginning every node has a different label).
At each round, each node updates its label according to some rule. The algorithm terminates as soon as no more updates.
LLP is built on APM (Absolute Potts Model) which is built on LPA => LLP iteratively executes APM with various $\gamma$ values.
Implementation detail: the node order during rounds is random, hence there is no obstacle in updating several nodes in parallel.
Note: most of the time is spent on sampling values of $\gamma$ to produce base clusterings => you can reduce the numbers of $\gamma$ values to speed up the process.
Laxman Dhulipala, Igor Kabiljo, Brian Karrer, Giuseppe Ottaviano, Sergey Pupyrev, Alon Shalita (2016): https://arxiv.org/abs/1602.08820
Previous work on compression techniques:
Inverted index (also known as postings file): database index storing a mapping from content (eg: word, content) to its location (eg: table, document). Allows fast full-text searches (use case: search engine indexing algorithm).
Graph reordering is a combinational optimization problem with a goal to find a layout (= order = numbering = arrangement) of the input graph to optimize a cost function: \(\pi\colon\mathbb V\to\mathbb {1 \ldots n}\)
Empiric insight: it is desirable that similar vertices are close in $\pi$.
Minimum linear arrangement (MLA): minimize \(\displaystyle\sum_{(u,v)\in E} |\pi(u) - \pi(v)|\)
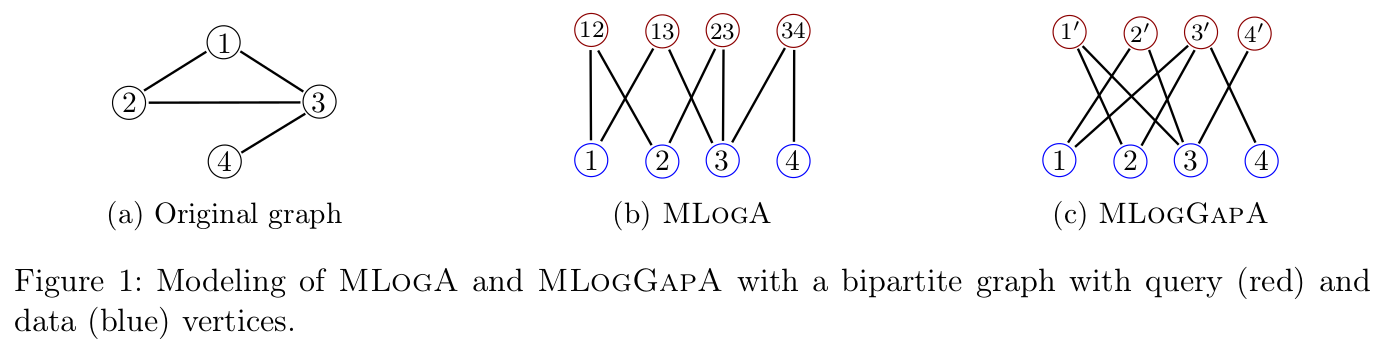
Minimum logarithmic arrangement (MLogA): minimize \(\displaystyle\sum_{(u,v)\in E} \log |\pi(u) - \pi(v)|\)
In practice, adjacency list is stored using an encoding, so the gaps induced by consecutive neighbors are important for compression hence the MLogGapA problem.
Minimum logarithmic gap arrangement (MLogGapA): minimize \(\displaystyle\sum_{u\in V} f_{\pi}(u, out(u))\) where \(f_{\pi}(u, out(u)) = \displaystyle\sum_{i=1}^{k} \log | \pi(u_{i+1}) - \pi(u_{i}) |\)
MLA and MLogA were known to be NP-Hard, this paper proves that MLogGapA is also NP-Hard.
Bipartite minimum logarithmic arrangement (BiMLogA): generalize MLogA and MLogGapA, minimize \(\displaystyle\sum_{q \in Q}\sum_{i=1}^{k} \log (\pi(u_{i+1}) - \pi(u_{i}))\) where $k$ is the degree, $Q$ query vertices, $D$ data vertices and the graph \(G = (Q \cup D, E)\).
Note: BiMLogA and MLogGapA differs since the latter does not distinguish between query and data vertices.

Graph bisection: initially split $D$ into two sets of same size $V_1$ and $V_2$, and compute a cost of how "compression-friendly" the partition is. Next, swap vertices in $V_1$ and $V_2$ to improve the cost (=> compute the "move gain").
Notes:
Main algorithm steps:
Time complexity: \(O(m\log n + n\log^2 n)\)
In the implementation, the algorithm can be parallelized/distributed:
Joel Mackenzie, Antonio Mallia, Matthias Petri, J. Shane Culpepper, and Torsten Suel (2019)
Note: focuses on inverted indexes more than graph
Goals:
Multiple ordering techniques:
BP ordering runs in \(O(m\log n + n\log^2 n)\) and yield excellent arrangements in practice by approximating the solution to the BiMLogA problem.
implementation/pseudo-code details
optimization details
Reproducibility notes: