Je vous donne un tableau possédant des trilliards d'éléments, et je
vous pose des milliards de questions de la forme : Quelle est la somme
des éléments compris entre l'indice \(i\) et \(j\) du tableau (avec \(i < j\)) ? La première idée d'algorithme
naïf que l'on peut avoir, est de parcourir pour chaque question les
éléments situés entre les indices donnés, et d'augmenter une variable
somme au fur et à mesure du parcours.
Cependant notre solution est bien trop longue pour le cas extrême donné en entrée, à cause des nombreux parcours que l'on réalise. Il nous faut donc une solution plus efficace, et une structure adaptée nous permettant de faire moins de parcours inutiles et ainsi raccourcir notre temps d'exécution : le tableau cumulatif.
Dans notre algorithme naïf, on utilise lors de nos parcours les informations récoltées uniquement pour répondre à une seule question parmi des milliards. Ceci nous oblige à repasser sur des parties du tableau déjà parcourue (voir le tableau en entier), résultant en un temps d'exécution trop élevé.
L'idée du tableau cumulatif (summed area table en anglais) est de parcourir une seule fois notre tableau entièrement, et d'utiliser les données récoltées pour ensuite répondre à n'importe quel type de question à propos de somme d'éléments contigus.
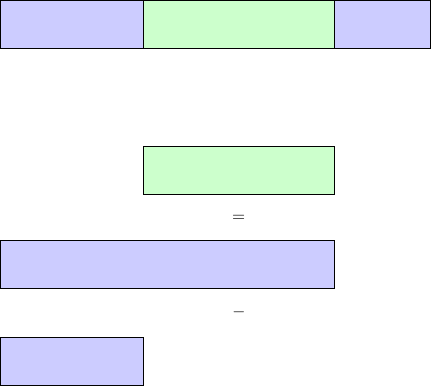
On peut très simplement expliquer son principe grâce à la géométrie et aux intervalles :

La partie verte dans le premier rectangle représente la question posée, et on voit qu'on peut retrouver exactement la même partie en utilisant deux sous parties du rectangle commençant toutes les deux au même endroit. L'avantage de pouvoir décomposer n'importe quelle sous partie du rectangle en deux autres ayant un début commun, est qu'on réduit alors le nombre de possibilités de sous parties. En effet, avec un début et une fin variables le nombre d'intervalles possibles est d'environ \(N^2\) (avec \(N\) le nombre d'éléments du rectangle), alors qu'avec un début d'intervalle fixe et uniquement une fin variable on arrive à \(N\) possibilités de sous parties.
Le principe du tableau cumulatif est justement de calculer tous les intervalles ayant un début fixe et une fin variable, afin de pouvoir connaitre rapidement n'importe quelle sous partie de notre tableau d'éléments.
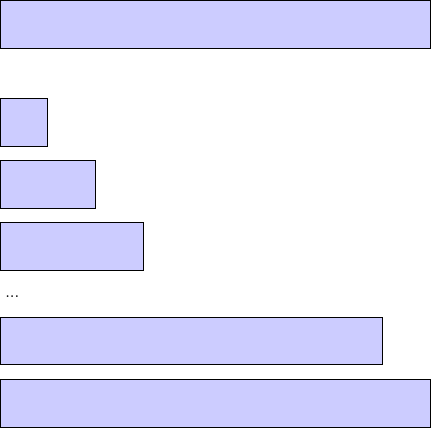
Afin de parfaitement comprendre l'utilisation d'un tableau cumulatif, prenons l'exemple de ce tableau : 26, 42, 1, 89, 3, 7.
À partir de la suite de nombres, on va créer un tableau cumulatif qui contiendra tous nos intervalles nécessaires, c'est-à-dire dans la première case l'élément 1, dans la deuxième case l'élément 1 + 2, dans la troisième case l'élément 1 + 2 + 3, etc.
| Tableau cumulatif |
|---|
| 26 |
| 26, 68 |
| 26, 68, 69 |
| 26, 68, 69, 158 |
| 26, 68, 69, 158, 161 |
| 26, 68, 69, 158, 161, 168 |
On a désormais notre tableau cumulatif 26, 68, 69, 158, 161, 168 que l'on va utiliser pour répondre à des questions du type quelle est la somme des éléments du tableau original entre deux indices \(i\) et \(j\) donnés. Il faut juste faire attention à une chose, c'est d'utiliser comme indice de début d'intervalle \(i - 1\) et non \(i\) car sinon notre premier élément ne sera pas inclus.
Question 1 : \(i = 3\) et \(j = 6\)
| Tableau | Tableau cumulatif |
|---|---|
| 26, 42, 1, 89, 3, 7 | 26, 68, 69, 158, 161, 168 |
On soustrait l'élément \(j\) (6ème) et l'élément \(i - 1\) (2ème), soit 168 - 68 = 100. Or on a bien dans notre tableau initial 1 + 89 + 3 + 7 = 100, la réponse est donc correcte.
Question 2 : \(i = 1\) et \(j = 4\)
| Tableau | Tableau cumulatif |
|---|---|
| 26, 42, 1, 89, 3, 7 | 26, 68, 69, 158, 161, 168 |
Ici l'indice 0 correspond à un résultat de 0, on a donc 158 - 0 = 158. Encore une fois, dans notre tableau, on retrouve bien le même résultat : 26 + 42 + 1 + 89 = 158.
Question 3 : \(i = 4\) et \(j = 5\)
| Tableau | Tableau cumulatif |
|---|---|
| 26, 42, 1, 89, 3, 7 | 26, 68, 69, 158, 161, 168 |
On a : 161 - 69 = 92 (or 89 + 3 = 92).
Question 4 : \(i = 1\) et \(j = 6\)
| Tableau | Tableau cumulatif |
|---|---|
| 26, 42, 1, 89, 3, 7 | 26, 68, 69, 158, 161, 168 |
De même : 168 - 0 = 168 (or 26 + 42 + 1 + 89 + 3 + 7 = 168).
Si l'on reprend notre énoncé dans l'introduction, on nous donne un tableau de taille \(N\), et \(M\) questions du type : Quelle est la somme des éléments de \(i\) à \(j\) dans le tableau ? Notre solution naïve, dans le pire des cas, aura une complexité en \(O(N \times M)\) (lorsqu'on parcourt à chaque fois le tableau en entier, soit quand \(i = 0\) et \(j = N\) pour chaque question). En revanche, notre tableau cumulatif revient à une complexité linéaire dans le pire des cas en \(O(N + M)\) car on parcourt une seule fois le tableau donné et pour répondre aux questions on a juste besoin d'accéder au tableau cumulatif (donc opération en \(O(1)\)).
Une implémentation en C d'un tableau cumulatif et de son utilisation :
#include <stdio.h>
#define TAILLE_MAX 1000
int tableau[TAILLE_MAX];
int cumulatif[TAILLE_MAX];
int nbElement;
void initTab(void)
{
int iEle;
scanf("%d\n", &nbElement);
for(iEle = 0; iEle < nbElement; ++iEle)
scanf("%d ", &tableau[iEle]);
}
void initCumulatif(void)
{
int iEle;
int dernier;
dernier = 0;
for(iEle = 0; iEle < nbElement; ++iEle) {
cumulatif[iEle] = tableau[iEle] + dernier;
dernier = cumulatif[iEle];
}
}
int somme(int debut, int fin)
{
if(debut == 0)
return cumulatif[fin];
else
return cumulatif[fin] - cumulatif[debut - 1];
}
int main(void)
{
initTab();
initCumulatif();
printf("%d\n", somme(2, 5));
printf("%d\n", somme(0, 3));
printf("%d\n", somme(3, 4));
printf("%d\n", somme(0, 5));
return 0;
}Quelques remarques sur le code :
initCumulatif.somme, j'admets que debut
est inférieur à fin et que les indices ne sont pas en
dehors du tableau pour simplifier le code.L'entrée :
6
26 42 1 89 3 7La sortie :
100
158
92
168Il est possible de répondre à des questions plus générales que sur la somme d'éléments, pour cela il suffit que notre opération possède une opération "inverse". Par exemple, l'inverse de l'addition est la soustraction (c'est d'ailleurs ce qu'on utilise dans notre tableau cumulatif, l'addition pour le construire, et la soustraction pour répondre aux questions), et l'inverse de la multiplication est la division. Il est donc possible de modifier le comportement de notre tableau cumulatif pour prendre en compte le produit d'une suite de nombre, la soustraction d'éléments contigus, etc. Le principe reste exactement le même, il suffit juste de changer la manière de construire et de répondre aux questions en fonction de l'opération choisie.
Le tableau cumulatif ne se limite pas à une seule dimension, on peut l'utiliser sur deux dimensions :
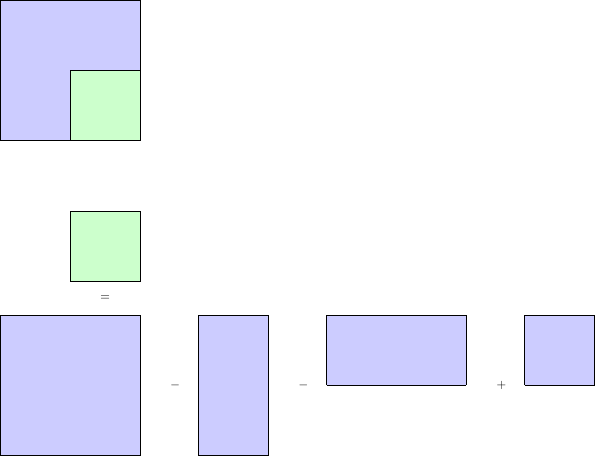
Le principe est toujours le même, mais il faut adapter nos fonctions qui construisent et répondent aux questions, pour qu'elles puissent fonctionner sur un tableau cumulatif en deux dimensions. Ici on remarque bien sur notre image que l'on cherche à retrouver n'importe quelle sous partie du rectangle en ayant un coin fixe (le coin en haut à gauche dans notre cas), pour de nouveau réduire le nombre de possibilités. Ce schéma nous montre comment répondre à une question sur un tableau cumulatif 2D, mais il faut surtout l'initialiser correctement afin de pouvoir l'utiliser :
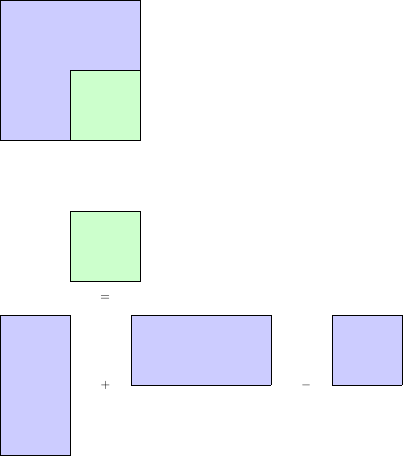
Une implémentation d'un tableau cumulatif 2D en C :
#include <stdio.h>
#define NB_LIG_MAX 1000
#define NB_COL_MAX 1000
int tableau[NB_LIG_MAX][NB_COL_MAX];
int cumulatif[NB_LIG_MAX][NB_COL_MAX];
int nbLig, nbCol;
void initTab(void)
{
int iLig, iCol;
scanf("%d %d\n", &nbLig, &nbCol);
for(iLig = 0; iLig < nbLig; ++iLig) {
for(iCol = 0; iCol < nbCol; ++iCol)
scanf("%d ", &tableau[iLig][iCol]);
scanf("\n");
}
}
void initCumulatif(void)
{
int iLig, iCol;
for(iLig = 0; iLig < nbLig; ++iLig) {
for(iCol = 0; iCol < nbCol; ++iCol) {
cumulatif[iLig][iCol] = tableau[iLig][iCol];
if(iLig - 1 >= 0)
cumulatif[iLig][iCol] += cumulatif[iLig - 1][iCol];
if(iCol - 1 >= 0)
cumulatif[iLig][iCol] += cumulatif[iLig][iCol - 1];
if(iLig - 1 >= 0 && iCol - 1 >= 0)
cumulatif[iLig][iCol] -= cumulatif[iLig - 1][iCol - 1];
}
}
}
int somme(int lig1, int col1, int lig2, int col2)
{
int resultat;
resultat = cumulatif[lig2][col2];
if(col1 - 1 >= 0)
resultat -= cumulatif[lig2][col1 - 1];
if(lig1 - 1 >= 0)
resultat -= cumulatif[lig1 - 1][col2];
if(lig1 - 1 >= 0 && col1 - 1 >= 0)
resultat += cumulatif[lig1 - 1][col1 - 1];
return resultat;
}
int main(void)
{
initTab();
initCumulatif();
printf("%d\n", somme(1, 1, 2, 2));
printf("%d\n", somme(0, 0, 3, 3));
printf("%d\n", somme(0, 0, 0, 3));
printf("%d\n", somme(3, 1, 3, 3));
return 0;
}L'entrée :
4 4
4 6 8 9
1 8 5 9
7 2 3 3
6 1 4 7On obtient en sortie :
18
83
27
12Le tableau cumulatif 2D ressemble à cela pour l'entrée :
4 10 18 27
5 19 32 50
12 28 44 65
18 35 55 83Le code suit exactement les deux schémas pour l'initialisation et pour l'utilisation du tableau cumulatif 2D. La complexité en temps cette fois est en \(O(N^2)\) pour l'initialisation et \(O(M)\) pour la réponse, contre une complexité pour la réponse de \(O(N^2 \times M)\) pour l'algorithme naïf.
Nous avons vu qu'il était possible de créer un tableau cumulatif sur une mais aussi deux dimensions, alors pourquoi pas sur \(N\) dimensions ? Techniquement, cela est possible, mais la représentation de \(N\) dimensions risque d'être très complexe et il sera alors difficile de visualiser le comportement de notre tableau cumulatif (initialisation et accès pour répondre aux questions). De plus, il est assez rare d'avoir besoin d'un tableau cumulatif au-delà de 3 dimensions, vu que nous ne percevons pas la 4ème.
Le tableau cumulatif est donc une structure de données permettant de connaître la somme d'éléments contigus rapidement, mais ce dernier ne se limite pas à la somme on peut aussi l'utiliser pour d'autres opérations comme la soustraction, la multiplication et la division, et on peut recréer cette structure en deux (ou même \(N\)) dimensions.