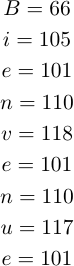
Tous les algorithmes de chiffrement symétriques ont un problème commun : la transmission de clé. Quel que soit l'algorithme utilisé, si la clé est interceptée par l'ennemi, alors il peut lire les communications, mais aussi se faire passer pour le destinataire et l'expéditeur du message. Ce problème est fondamental car transmettre une clé de chiffrement est très délicat, et même impossible dans certains cas (par exemple avec Internet, c'est compliqué d'aller voir physiquement le responsable de chaque serveur pour qu'il vous transmette une clé), il était donc nécessaire de trouver une autre solution face à ce problème : les chiffrements asymétriques.
L'idée du chiffrement asymétrique est d'utiliser deux clés au lieu d'une, que l'on va attribuer à chaque personne :
Les bases du chiffrement asymétrique furent introduites par Whitfield Diffie et Martin Hellman en 1976, lorsqu'ils ont montré comment résoudre le problème d'échange de clés de manière sécurisée. La particularité de ce système est qu'il est simple de générer des couples de clés, mais quasiment impossible de retrouver la clé privée à partir de la clé publique.
En 1977 l'algorithme RSA est présenté, et sera l'un des premiers systèmes de chiffrement asymétriques utilisant ce concept de paires de clés et à en faire une implémentation possible pour la communication de messages grâce à des principes mathématiques. Cet algorithme est encore très utilisé de nos jours, surtout sur Internet (dans le commerce en ligne, les transactions sécurisées, etc.) et constitue la base de quasiment tous les systèmes de chiffrement modernes.
L'algorithme RSA va dans un premier temps générer deux couples de clés asymétriques, l'un pour l'**émetteur** qu'on appellera Alice, et l'autre pour le destinataire qu'on appellera Bob. Une fois que chaque personne a ses deux clés, on peut procéder à une communication sécurisée. Alice va chercher la clé publique de Bob (en général on pratique à un échange des clés publiques avant de communiquer, ou alors on les diffuse publiquement), et elle va chiffrer son message avec. Ensuite le message chiffré est transmis à Bob, et il va le déchiffrer grâce à sa clé privée (qu'il n'a communiqué à personne). Aucun échange de clé sensible n'est nécessaire, et seule la clé privée de Bob peut déchiffrer le message, la communication est alors sécurisée.
La sécurité de l'algorithme se trouve dans l'utilisation d'une fonction de chiffrement et de déchiffrement à sens unique. Cette fonction est, comme pour la génération de clé, très simple à appliquer dans un sens (avec la clé privée), mais extrêmement complexe dans l'autre (sans la clé privée).
Tout d'abord, regardons comment générer nos clés :
La clé publique correspond au couple (\(n\), \(e\)) et la clé privée au couple (\(n\), \(d\)).
Pour chiffrer notre message, on utilisera alors cette relation :
\(f(x) = x^e \mod n\)
Avec \(x\) le message en clair, et \(f(x)\) le message chiffré.
Et pour le déchiffrement, on utilise la fonction suivante :
\(f'(x) = x^d \mod n\)
Avec cette fois \(x\) le message chiffré et \(f'(x)\) le message déchiffré.
Choisissons comme message "Bienvenue", et chiffrons-le avec l'algorithme RSA.
La première étape est de générer notre clé publique et privée car je n'en possède pas encore, et comme je n'ai pas d'ami nommé Bob à qui envoyer des messages secrets, je vais m'envoyer le message chiffré à moi-même (pour simplifier les explications et ne pas être embrouillé dans toutes les valeurs numériques). On applique donc notre algorithme de création de clés :
Soit \(p\) et \(q\) deux nombres premiers que je choisis aléatoirement :
\(p = 61\) et \(q = 137\)
À partir de cela, on peut calculer notre module de chiffrement :
Ainsi que l'indicatrice d'Euler de \(n\) :
Ensuite, il faut choisir notre exposant de chiffrement \(e\) qui doit être premier avec \(m\) et strictement inférieur à ce dernier, je choisis donc 7 :
\(e = 7\)
Désormais nous devons trouver notre exposant de déchiffrement. Cette partie est un peu plus compliquée, car elle nécessite quelques notions de maths.
On cherche donc \(d\) qui est l'inverse modulaire de \(e \mod m\), on a :
\(d \equiv e^{-1} \pmod m\)
Ce qui est équivalent à :
\(de \equiv 1 \pmod m\)
Par définition de la congruence, \(m\) est un diviseur de \(d e - 1\), ce qu'on peut écrire comme ceci :
\(de - 1 = qm\) avec \(q\) le quotient de \(\frac{(de - 1)}{m}\)
On a finalement :
\(de - qm = 1\)
On connait \(e\), \(m\), et on cherche \(d\) :
On remarque que cette expression est de la forme de l'identité de Bézout \(ax + by = pgcd(a, b)\) avec \(a = e\), \(b = m\), \(x = d\), \(y = -q\), et \(e\) et \(m\) sont premiers entre eux donc \(pgcd(a, b) = 1\). Or on peut trouver les coefficients \(x\) et \(y\) (et donc \(d\), qui nous intéresse) grâce à l'algorithme d'Euclide étendu. Une implémentation de cet algorithme pour ceux que ça intéresse :
#include <stdio.h>
void euclideEtendu(int a, int b)
{
int r0, r1;
int s0, s1;
int t0, t1;
int i;
int q, r, s, t;
r0 = a;
s0 = 1;
t0 = 0;
r1 = b;
s1 = 0;
t1 = 1;
r = 42;
for(i = 2; r != 0; ++i) {
q = r0 / r1;
r = r0 - q * r1;
s = s0 - q * s1;
t = t0 - q * t1;
r0 = r1;
r1 = r;
s0 = s1;
s1 = s;
t0 = t1;
t1 = t;
}
printf("x = %d\n", s0);
printf("y = %d\n", t0);
}
int main(void)
{
int a, b;
scanf("%d %d\n", &a, &b);
euclideEtendu(a, b);
return 0;
}L'entrée :
7
8160La sortie :
x = -3497
y = 3On trouve grâce au dernier programme :
\(d = -3497\)
On a désormais \(d\) vérifiant l'équation \(de \equiv 1 \pmod m\). Cependant, on préfèrera travailler avec des nombres positifs, et selon Wikipédia le coefficient \(x\) n'est pas unique (\(y\) non plus mais c'est \(x\) qui nous intéresse), et on peut en trouver une infinité qui respectent la relation suivante :
\(x + k\frac{b}{pgcd(a, b)}\) avec \(k\) un nombre entier relatif
Si on remplace par nos valeurs (\(x = d\), \(b = m\), \(pgcd(a, b) = 1\)), on obtient :
\(d + km\)
Et avec les valeurs numériques :
\(-3497 + 8160k\)
On veut donc trouver un nombre \(d\) positif :
Or \(k\) est un nombre entier, je vais donc arrondir à l'entier supérieur \(k = 1\) pour avoir une valeur de \(d\) positive :
Notre couple de clé publique/privée est désormais généré :
On peut maintenant chiffrer et déchiffrer notre message avec nos clés en appliquant les fonctions :
Les caractères seront représentés par des nombres grâce à la table ASCII permettant de résoudre les relations mathématiques (on imagine dans notre cas que les caractères du message sont tous présents dans la table ASCII pour simplifier le problème).
Notre message correspond donc à ceci selon la table ASCII :
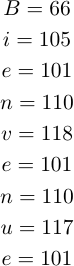
Le message chiffré :

On se retrouve avec un message ressemblant à ceci
2546 824 4962 8071 2160 4962 8071 5933 4962 Que l'on peut déchiffrer :

On retrouve bien nos valeurs numériques que l'on peut facilement transformer en caractères pour former notre message original.
Le pseudo-code de l'algorithme RSA :
cléPublique(p, q) :
Choisir aléatoirement p et q, deux nombres premiers distincts
n = p * q
m = (p - 1) * (q - 1)
Choisir e strictement inférieur à m et premier avec lui
Retourner couple (n, e)
cléPrivée(e, m, n) :
Algorithme d'Euclide étendu pour calculer d (l'inverse de la multiplication
de e mod m)
Retourner couple (n, d)
chiffrer :
Pour chaque caractère du message
lettreChiffrée = lettreClaire ^ e mod n
déchiffrer :
Pour chaque caractère du message
lettreClaire = lettreChiffrée ^ d mod n Une dernière question se pose cependant face à ce pseudo-code : comment calculer des nombres avec des puissances aussi énormes ? En effet, \(d = 4663\) dans notre exemple et élever un nombre à la puissance 4663 est tout simplement fou (surtout qu'en situation réelle, notre \(e\) et \(d\) peuvent comporter plusieurs centaines de chiffres chacun). Si on calcule séparément \(a^b\) puis on applique le modulo \(c\) sur le résultat on sera confronté à un problème de stockage car quand \(b\) est grand le résultat \(a^b\) sera tellement gigantesque que notre programme ne pourra pas stocker ce nombre. Heureusement un algorithme nous permet de calculer facilement le résultat d'une opération du style \(a^b \mod c\), c'est l'exponentiation modulaire.
Soit \(x = a^b \mod c\), on peut trouver \(x\) facilement grâce à notre nouvel algorithme :
x = 1
Pour chaque exposant allant de 1 à b inclus
x = (x * a) mod cCet algorithme nous permet donc de travailler avec des nombres bien plus petits qui ne dépasseront jamais \(c\) car à chaque multiplication on effectue un modulo dessus.
Une implémentation en C de l'algorithme de RSA :
#include <stdio.h>
#include <time.h>
#include <stdlib.h>
#define TAILLE_MAX 1000
unsigned long long message[TAILLE_MAX];
int taille;
// Clé
int p, q;
int n;
int m;
int e, d;
int PGCD(int a, int b)
{
int r;
while(b != 0) {
r = a % b;
a = b;
b = r;
}
return a;
}
int euclideEtendu(int a, int b)
{
int r0, r1;
int s0, s1;
int t0, t1;
int i;
int q, r, s, t;
r0 = a;
s0 = 1;
t0 = 0;
r1 = b;
s1 = 0;
t1 = 1;
r = 42;
for(i = 2; r != 0; ++i) {
q = r0 / r1;
r = r0 - q * r1;
s = s0 - q * s1;
t = t0 - q * t1;
r0 = r1;
r1 = r;
s0 = s1;
s1 = s;
t0 = t1;
t1 = t;
}
return s0;
}
void clePublique(void)
{
static int premier[] = {2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,
47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97, 101, 103, 107, 109, 113, 127,
131, 137, 139, 149, 151, 157, 163, 167, 173, 179, 181, 191, 193, 197, 199,
211, 223, 227, 229, 233, 239, 241, 251, 257, 263, 269, 271, 277, 281, 283,
293, 307, 311, 313, 317, 331, 337, 347, 349, 353, 359, 367, 373, 379, 383,
389, 397, 401, 409, 419, 421, 431, 433, 439, 443, 449, 457, 461, 463, 467,
479, 487, 491, 499, 503, 509, 521, 523, 541};
/*do
{
p = premier[rand() % 100];
q = premier[rand() % 100];
} while(p == q);*/
p = 61;
q = 137;
n = p * q;
m = (p - 1) * (q - 1);
for(e = 2; PGCD(e, m) != 1; ++e)
;
}
void clePrivee(void)
{
d = euclideEtendu(e, m);
while(d < 0)
d += m;
}
void chiffrement(void)
{
int iMessage, iExp;
int lettre;
for(iMessage = 0; iMessage < taille; ++iMessage) {
// Exponentiation modulaire
lettre = message[iMessage];
message[iMessage] = 1;
for(iExp = 1; iExp <= e; ++iExp)
message[iMessage] = (message[iMessage] * lettre) % n;
}
}
void dechiffrement(void)
{
int iMessage, iExp;
int lettre;
for(iMessage = 0; iMessage < taille; ++iMessage) {
// Exponentiation modulaire
lettre = message[iMessage];
message[iMessage] = 1;
for(iExp = 1; iExp <= d; ++iExp)
message[iMessage] = (message[iMessage] * lettre) % n;
}
}
int main(void)
{
char iCar;
int iMessage;
// Lit le message et le transforme en nombre
iMessage = 0;
do
{
scanf("%c", &iCar);
if(iCar != '\n') {
message[iMessage] = (unsigned long long)iCar;
++iMessage;
}
} while(iCar != '\n');
taille = iMessage;
// Génère le couple de clé
srand(time(NULL));
clePublique();
clePrivee();
printf("Cle publique : %d %d\n", n, e);
printf("Cle privee : %d %d\n", n, d);
// Chiffre le message et l'affiche comme une suite de nombre
chiffrement();
for(iMessage = 0; iMessage < taille; ++iMessage)
printf("%llu ", message[iMessage]);
printf("\n");
// Déchiffre le message et l'affiche comme une chaîne
dechiffrement();
for(iMessage = 0; iMessage < taille; ++iMessage)
printf("%c", (char)message[iMessage]);
printf("\n");
return 0;
}Quelques remarques sur le code :
unsigned long long qui est le
type le plus grand en C (il stocke des nombres allant de \(0\) à \(2^{64} -
1\)), car un int ne sera pas toujours suffisant, on
prend donc des précautions en utilisant un type de données très grand
pour ne pas avoir de problèmes. Sachez qu'en C, il existe la
bibliothèque GMP pour manipuler de
très grands nombres.clePublique, j'utilise un tableau
statique contenant tous les nombres premiers de 1 à 100 et je tire au
sort pour déterminer \(p\) et \(q\) (j'ai rentré directement
p = 61 et q = 137 pour que les résultats
concordent avec notre exemple, mais la partie tirage au sort est
commentée).char après le déchiffrement
pour afficher une chaîne de caractères.Le message d'entrée :
BienvenueLa sortie :
Cle publique : 8357 7
Cle privee : 8357 4663
2546 824 4962 8071 2160 4962 8071 5933 4962
BienvenueIl est important de noter que recréer sa propre implémentation de RSA (ou même de n'importe quel algorithme de chiffrement) dans le but de l'utiliser dans une application concrète est une mauvaise idée, et il est conseillé d'utiliser des implémentations déjà existantes, libres, accessibles à tous et qui sont utilisées par des milliers d'autres personnes comme : OpenSSL, GnuPG, etc. L'avantage d'utiliser ce genre d'outils est que de nombreuses personnes travaillent dessus chaque jour, et des recherches sont effectuées régulièrement pour découvrir les potentielles failles afin de rendre le système encore plus robuste.
Cette partie n'est pas essentielle pour comprendre le fonctionnement de l'algorithme, mais permet aux curieux de voir comment démontrer que notre système marche. Plusieurs notions mathématiques sont nécessaires pour la compréhension de la démonstration, mais sachez que j'ai appris au fur et à mesure en rédigeant cette partie sans connaitre à l'avance les outils mathématiques utilisés, donc il est tout à fait possible qu'un lecteur fasse de même s'il est vraiment intéressé par le sujet.
C'est bien beau toutes ces explications, mais mathématiquement comme être sûr que notre algorithme marche à tous les coups ? Comment savoir si notre message original une fois chiffré sera le même quand il est déchiffré ?
Pour cela il faut prouver que l'algorithme RSA est valide, on part donc des deux fonctions de chiffrement et de déchiffrement :
Dire que notre algorithme est valide revient à prouver que :
\(f(f'(x)) = f'(f(x)) = x \mod n\)
Cependant on remarque que :
Et :
On a \(f(f'(x)) = f'(f(x)) = x^{ed} \mod n\), et on cherche donc à démontrer que \(x^{ed} \equiv x \pmod{pq}\) (car \(n = pq\)). Or d'après le théorème des restes chinois, pour démontrer la congruence \(pq\), il suffit de démontrer les congruences \(p\) et \(q\) séparément. Démontrons d'abord que \(x^{ed} \equiv x \pmod p\) :
On va diviser le problème en deux cas, soit \(x\) est divisible par \(p\), soit il ne l'est pas, donc soit \(x \equiv 0 \pmod p\), soit \(x \not\equiv 0 \pmod p\), commençons par le premier cas (qui est le plus simple) :
\(x\) est un multiple de \(p\), donc \(x^{ed} \equiv 0 \pmod p\), or \(x \equiv 0 \pmod p\), donc \(x^{ed} \equiv x \pmod p\).
On continue avec notre deuxième cas où \(x\) n'est pas divisible par \(p\) :
Tout d'abord, par définition de \(e\), \(d\) et \(m\) :
Ceci signifie que \((p - 1)(q - 1)\) est un diviseur de \(ed - 1\), on a :
\(ed = 1 + k(p - 1)(q - 1)\) avec \(k\) un nombre entier représentant le quotient de \(\frac{(ed - 1)}{(p - 1)(q - 1)}\)
Donc :
Et d'après le théorème de Fermat \(x^{p - 1} \equiv 1 \pmod p\) :
Donc pour tout \(x\), on a \(x^{ed} \equiv x \pmod p\). La démonstration pour la congruence de \(q\) est exactement la même. On a démontré que \(x^{eq} \equiv x \pmod{pq}\), et donc que \(x^{eq} \equiv x \pmod n\), donc notre algorithme vérifie l'équation au départ confirmant la validité de RSA.
Si vous êtes observateur, vous avez peut-être remarqué que finalement
le message chiffré obtenu est le résultat d'une simple substitution
mono-alphabétique et que par conséquent chaque lettre sera toujours
chiffrée de la même façon. Ceci est grave car notre message ne va pas
résister longtemps à une cryptanalyse basique. Prenons l'exemple du
message "Bienvenue", on a obtenu le résultat suivant
2546 824 4962 8071 2160 4962 8071 5933 4962, cependant ce
message a été chiffré avec une clé publique, et donc comme n'importe qui
peut accéder à cette clé, il est facile d'établir un tableau de
correspondance en chiffrant chaque lettre de l'alphabet avec la clé
publique afin de déduire à quelle lettre de l'alphabet correspond notre
lettre du message chiffré. Ce problème est dû au fait que l'on peut
distinguer les différentes lettres dans notre message chiffré, si ce
n'était pas le cas on aurait aucunes informations sur la clé privée
utilisée ou encore sur le message déchiffré.
Il est donc nécessaire de procéder autrement afin de sécuriser le message en lui-même et en rendant impossible tout cryptanalyse dessus. Si vous utilisez l'algorithme RSA, il y a de fortes chances que vous êtes sur un ordinateur, cependant sur un ordinateur tout est stocké à l'aide de bit (une simple unité valant soit 0 soit 1, permettant de compter en base binaire), un groupe de 8 bits est appelé un octet. Quand votre ordinateur stocke une chaîne de caractères, il stocke en réalité une succession d'octets formant chaque lettre, par exemple dans la table ASCII on peut utiliser un seul octet pour représenter les 128 valeurs car elles ne nécessitent que 7 bits pour être stockées. En sachant cela, on sait qu'une suite d'octet peut être interprétée comme une chaîne car pour notre ordinateur tout est un nombre, c'est nous qui lui disons que tel caractère correspond à tel octet (et inversement) avec des tables comme celle ASCII. On pourrait donc représenter notre message non plus comme une suite d'octet mais comme un groupe d'octet uni, ce qui fait qu'au lieu de chiffrer chaque octet un par un, on chiffre le tout d'un seul coup, rendant alors la cryptanalyse impossible (avec l'ancien système un octet pouvait valoir une des 128 valeurs, mais désormais notre groupe d'octet réuni peut prendre un nombre considérable de valeurs différentes qui augmente avec la taille du message). Il n'y a aucun moyen de trouver des informations à cause de ce groupement, et la seule solution est d'essayer toutes les combinaisons, mais vu le nombre de possibilités, on se rend vite compte que c'est impossible. Prenons par exemple le message "Code" :
| Lettre | C | o | d | e |
|---|---|---|---|---|
| Hexadécimale | 0x43 | 0x6F | 0x64 | 0x65 |
| Décimale | 67 | 111 | 100 | 101 |
J'utilise la notation hexadécimale car
cette dernière permet de stocker un octet plus simplement qu'en notation
décimale. Notre message devient alors la suite d'octet
0x436F6465 (ce nombre correspond à 1131373669 en décimal)
que notre ordinateur peut tout à fait comprendre si on lui indique
d'afficher cette suite comme une chaîne. Donc au lieu de chiffrer les
nombres 0x43, 0x6F, 0x64,
0x65 séparément on va plutôt chiffrer
0x436F6465 uniquement. Puisqu'on sait que notre message
utilise la table ASCII et que cette dernière n'a besoin que d'un octet
pour représenter toutes les valeurs possibles, on sait qu'une lettre en
notation hexadécimale ne prendra pas plus de deux caractères (si on
exclut le 0x qui est juste là pour indiquer que c'est de
l'hexadécimal). On peut donc une fois notre nombre déchiffré, le
découper en plusieurs nombres (toujours représentés en notation
hexadécimale) que l'on va convertir en caractère grâce à la table
ASCII.
En C par exemple, il est facile de convertir une chaîne en un nombre hexadécimal et inversement :
#include <stdio.h>
#include <string.h>
#include <stdlib.h>
#define TAILLE_MAX 1000
int main(void)
{
char message[TAILLE_MAX];
char hexa[TAILLE_MAX * 2];
char caractere[8];
int iMessage, ihexa;
scanf("%[^\n]s\n", message);
// Transformation du message en une chaîne représentant notre nombre hexadécimal
for(iMessage = 0; message[iMessage] != '\0'; ++iMessage) {
sprintf(caractere, "%x", message[iMessage]);
strcat(hexa, caractere);
}
printf("0x%s\n", hexa);
// Transformation en une chaîne de caractère lisible
for(ihexa = 0; hexa[ihexa] != '\0'; ihexa += 2) {
char lettre[3];
lettre[0] = hexa[ihexa];
lettre[1] = hexa[ihexa + 1];
lettre[2] = '\0';
printf("%c", (int)strtoul(lettre, NULL, 16));
}
printf("\n");
return 0;
}On peut utiliser le spécificateur x dans printf afin
de convertir notre lettre en nombre hexadécimal. De même, on peut
utiliser stroul
afin de convertir notre nombre hexadécimal en base 10 et de l'afficher
comme un caractère.
En entrée par exemple du programme :
CodeOn obtient bien en sortie notre message sous forme d'un nombre hexadécimal :
0x436f6465
CodeCependant quand notre message est important, le nombre obtenu est beaucoup trop grand pour être chiffré, il faut alors découper notre message en plusieurs sous nombres hexadécimaux au lieu d'un seul et appliquer le même principe de chiffrement/déchiffrement.
Désormais qu'on sait que notre message peut être sécurisé, il ne nous reste plus qu'à prouver que notre système de clé asymétrique est fiable car si l'ennemi arrive à calculer la clé privée, il peut déchiffrer le message simplement sans avoir à le casser.
Tout le monde peut théoriquement accéder à la clé publique d'une personne et donc peut connaître \(n\) et \(e\), mais cela est-il réellement un problème ? Car pour avoir la clé privée il faut trouver \(d\) puisqu'on connait déjà \(n\), or pour trouver \(d\), il nous faut \(e\) (que l'on a), mais surtout \(m\). Pour rappel \(m = (p - 1) \times (q - 1)\), et les seules informations qu'on pourrait avoir sur \(p\) et \(q\) peuvent venir de \(n\) car \(n = p \times q\). Il faudrait donc factoriser \(n\) en ses deux facteurs premiers \(p\) et \(q\). Et c'est là que l'histoire se complique, car s'il est facile de trouver et de multiplier deux nombres premiers entre eux, il l'est beaucoup moins pour décomposer en produit de facteurs premiers. Aujourd'hui, personne n'a encore trouvé d'algorithme qui s'exécute en temps polynomial, et le meilleur algorithme qu'on connaisse a une complexité exponentielle (et qui ressemble à ça pour les curieux : \(O(\exp((\frac{64b}{9})^{\frac{1}{3}}(\log b)^{\frac{2}{3}}))\) avec \(b\) le nombre de bit de notre nombre \(n\)). Cependant, la question de l'existence d'un algorithme efficace de décomposition d'un nombre en ses facteurs premiers reste encore ouverte et pourrait jouer un rôle majeur en cryptographie si la réponse était découverte. En attendant, on peut jouer sur le fait qu'il est donc très long de décomposer \(n\), et qu'il faudrait beaucoup de moyens pour trouver une clé de chiffrement privée en un temps raisonnable. C'est pourquoi il faut choisir la taille de ses clés avec attention et les renouveler si possible régulièrement.
Aujourd'hui une clé est "sécurisée" si elle contient entre 2048 et 4096 bits, mais "sécurisé" n'est pas entre guillemets pour rien car certes votre voisin sera incapable de casser votre clé, certes votre groupe de hacker préféré non plus (à part s'ils ont des moyens colossaux à leur disposition), mais par contre une agence gouvernementale pourrait éventuellement y arriver. En effet des agences comme la NSA ont d'énormes moyens techniques mis en œuvre (qui évoluent, mais dont on a une petite idée grâce aux révélations de Snowden en 2013), et même si sur une grande échelle ils ne peuvent pas casser toutes les clés aussi importantes que cela, il est possible pour eux de casser quelques-unes en particulier si elles sont d'un très haut niveau d'importance. Pour cela, l'agence utilise des superordinateurs qui souvent sont construits et optimisés spécifiquement dans le but de casser telle ou telle clé, et ils investissent des millions (voir des milliards selon leur budget annuel) dans la recherche afin de trouver une factorisation en un temps raisonnable (d'environ un an en général). En plus de cela, l'agence peut faire des pressions sur des organisations contenant des données sensibles, on retiendra notamment l'affaire lavabit où la NSA a obligé le créateur de ce service de mail chiffré à divulguer des informations secrètes à propos d'Edward Snowden. Le créateur ne pouvait en aucun cas parler de cette affaire au grand public sous peine d'emprisonnement et d'amende considérable, et fut finalement forcé de fermer son système de communication afin de ne pas coopérer avec la NSA. De nombreuses autres affaires de pression de la part de la NSA ou de gouvernements en général existent, et elles montrent bien la détermination de certaines agences dans le but de trouver les clés privées de certains individus.
Ce qu'il faut retenir de cela, est qu'il est nécessaire pour avoir un système sécurisé d'utiliser des clés importantes en taille et que l'on renouvelle régulièrement.
À moins que vous ayez de gros problèmes avec la NSA, votre clé devrait normalement être sécurisée si elle est assez longue. Mais il reste encore une faille dans notre système c'est la transmission de la clé publique. En effet, cette communication peut être compromise si quelqu'un se fait passer pour vous, et l'usurpation d'identité est résolue grâce à une signature numérique (comme lorsque vous signez un papier administratif dans la vraie vie pour vous identifier).
Le principe est plutôt simple, on a vu que pour un message \(x\), on a \(f(f'(x)) = f'(f(x)) = x \mod n\). Lorsqu'on veut signer notre message et certifier que c'est nous qui l'avons envoyé, on va dans un premier temps chiffrer notre message avec notre clé privée, puis on le chiffre de nouveau avec la clé publique de la personne à qui on souhaite envoyer le message. Une fois que la personne le reçoit, elle va déchiffrer avec sa clé privée le message puis, elle va le déchiffrer de nouveau avec votre clé publique (car on a chiffré dans un premier temps avec notre propre clé privée). Si le message a un sens, cela confirme que c'est bien vous qui l'avais envoyé car vous êtes le seul à connaître votre clé privée.
Malheureusement, sur de grands messages, cela prend beaucoup de temps de chiffrer et déchiffrer deux fois au lieu d'une. On a donc eu l'idée d'utiliser une fonction de hachage, cette fonction prend en entrée un message, un nombre, une image, etc. et lui associe une empreinte unique de taille fixe (il suffit de changer une partie minime du message pour avoir une empreinte totalement différente), et cette empreinte ne permet en aucun cas de retrouver l'entrée de la fonction de hachage. Il est possible que vous en ayez déjà entendu parler ou même utiliser si par exemple vous utilisez Linux car lorsque vous téléchargez l'image d'une distribution, il est souvent possible de vérifier l'intégrité et la validité de l'image grâce à un programme utilisant une fonction de hachage comme SHA-1 ou encore MD5. On va donc donner à notre fonction de hachage notre message en clair, et on va chiffrer une première fois l'empreinte avec notre clé privée, puis on la joint au message que l'on veut transmettre, et on chiffre le tout comme un message normal avec la clé publique du destinataire avant de l'envoyer. Une fois que la personne reçoit le message, elle le déchiffre avec sa clé privée et déchiffre l'empreinte jointe avec la clé publique de l'émetteur, elle va ensuite vérifier l'empreinte en réalisant une de son côté (avec la même fonction de hachage que celle utilisée par l'émetteur). Si l'empreinte est la même alors on est sûr que le message est complet, non modifié et provient bien du destinataire, sinon c'est qu'il a été corrompu. Cette méthode est bien plus courte et rapide car on chiffre/déchiffre uniquement deux fois l'empreinte et non pas le message entier.
Notre système est donc théoriquement sécurisé, et le seul moyen que l'on connait pour le moment est d'investir beaucoup d'argent et de temps pour factoriser \(n\). Cependant, tout le monde n'utilise pas RSA à la perfection, et on peut trouver certaines failles dans des utilisations de cet algorithme qui permettent d'autres types d'attaques.
Imaginons qu'Alice souhaite communiquer avec Bob, pour cela ils s'échangent leurs clés publiques. Cependant, Carole qui est une méchante personne, intercepte la clé publique de Bob qu'il a envoyée à Alice, et Carole va envoyer sa propre clé publique. Désormais, lorsqu'Alice va chiffrer son message avec la soi-disant clé de Bob, elle le chiffre en réalité avec celle de Carole, ce qui signifie que lorsque Alice envoie un message chiffré à Bob, si Carole l'intercepte elle va déchiffrer le message, le lire, potentiellement le modifier, et le chiffrer avec la clé publique de Bob avant de lui renvoyer. Ainsi, Alice et Bob ne se doutent de rien et pensent que leur communication est sécurisée, mais Carole a pu lire et modifier leurs messages.
Cette attaque peut être extrêmement gênante, et avec Internet c'est encore plus simple de la réaliser car vous n'êtes jamais réellement sûr que votre communication va directement au serveur sans passer par un autre ordinateur ennemi. Mais on peut contrer cette attaque grâce à plusieurs techniques, tout d'abord l'utilisation d'un annuaire contenant toutes les clés publiques de chaque personne ne nécessiterait plus la communication de clés. Cependant, il est possible que Carole soit très puissante et soit capable de modifier cet annuaire, on pourrait alors penser à plusieurs solutions comme un système d'identification physique (empreinte digitale, reconnaissance faciale, reconnaissance de l'iris, authentification par biométrie, etc.), ou encore une transmission manuelle dans une valise diplomatique par exemple. Mais toutes ces propositions ne sont pas applicables dans tous les domaines, sur Internet encore une fois on ne peut pas se permettre de se baser sur une identification physique d'un serveur, c'est alors qu'apparait les autorités de certifications. L'idée est d'utiliser une personne intermédiaire que l'émetteur et le destinataire font confiance, qui se chargera de la transmission des clés, mais pour être sûr de la sécurité on va en utiliser plusieurs qui à la chaîne se transmettent les clés et se font confiance. On crée alors plusieurs couches de sécurité lors de la transmission de la clé publique aux autorités de certification, et c'est d'ailleurs sur quoi sont basés les protocoles de sécurité SSL/TLS largement utilisés sur Internet et qui ont permis la création du protocole HTTPS. Malheureusement, des organisations gouvernementales (oui encore la NSA), peuvent faire pression sur certaines autorités de certifications afin d'utiliser l'attaque de l'homme du milieu, et l'une des seules solutions à ce problème est d'utiliser un service décentralisé (là où les autorités doivent certifier une autre autorité, notre système décentralisé demande que les deux autorités se certifient mutuellement). Le fait que le système soit décentralisé rend bien plus compliqué les attaques de ce genre, car chaque autorité peut classer une autre comme étant totalement de confiance, peu de confiance ou encore frauduleuse. Plus le niveau de classification de la confiance est bas, plus l'autorité doit avoir de retours positifs de la part d'autres autorités de confiance afin de valider la transmission des clés. Si une autorité de certification est corrompue, les autres ne lui feront plus confiance et vu qu'une confiance mutuelle est nécessaire, cette autorité sera mise de côté voir plus du tout utilisée. On a donc un réseau totalement décentralisé permettant plus de sécurité, et évitant un système de pression de la part d'organisations ayant beaucoup d'influence.
À la création du système RSA, les ordinateurs étaient loin d'être aussi rapides qu'aujourd'hui et ce problème d'efficacité était réellement compromettant. Pour permettre un algorithme plus rapide, on utilisait souvent des valeurs de \(e\) petites (3, 7, 17, etc.) afin d'améliorer le temps nécessaire à l'algorithme pour générer des paires de clés et de chiffrer le message. Cependant, Johan Håstad démontra en 1985, que si on envoyait un même message à au moins \(e\) personnes avec le même exposant, alors on pouvait déchiffrer le texte facilement. Vu qu'en général on utilisait des exposants comme \(e = 3\), il suffisait alors d'intercepter 3 mêmes messages qu'une personne a envoyé à différents destinataires, pour en trouver le contenu déchiffré. Pour effectuer cette attaque, le mathématicien a utilisé le théorème des restes chinois :
Imaginons, qu'Alice envoie à au moins 3 personnes un même message chiffré, avec le même exposant \(e = 3\). Soit les trois messages chiffrés \(c_1\), \(c_2\), \(c_3\), leurs modules de chiffrement respectifs \(n_1\), \(n_2\), \(n_3\), et le message déchiffré \(d\). On a démontré que \(f'(f(d)) = d \mod n\), ce qui signifie que déchiffrer un message chiffré revient à exprimer \(d \mod n\). On a donc \(c_i \equiv d^3 \mod n_i\) avec \(i\) allant de 1 à 3. Grâce au théorème des restes chinois, on peut trouver un nombre \(c\) tel que \(c_i \equiv c \mod n\), ce qui nous donne \(c \equiv d^3 \mod{n_1 n_2 n_3}\). Or par définition, \(d < n_i\), et donc \(d^3 < n_1 n_2 n_3\). Alors on peut écrire \(c = d^3\), et calculer \(d\) facilement \(d = \sqrt[3]{c}\). On peut généraliser cette attaque en remplaçant 3 par \(e\), mais plus \(e\) est grand plus l'attaque est difficile à mettre en place.
Cette attaque sera ensuite reprise par plusieurs autres mathématiciens pour créer différentes variantes et améliorations : Franklin-Reiter, Coppersmith.
Ceci nous montre bien que dans ce cas, à défaut de vouloir utiliser l'algorithme plus rapidement, on perd énormément en sécurité, il faut donc faire attention lors d'amélioration de ce type à ne pas affaiblir le système de chiffrement. Un petit exposant \(e\) facilite donc cette attaque, car plus il est petit plus le nombre de messages à récupérer est faible, et plus le temps nécessaire à trouver le message déchiffré est court. Pour se protéger face à cette attaque, il suffit d'utiliser un exposant \(e\) assez important.
Dans le même style qu'attaquer des messages avec des \(e\) petits, en 1990 Michael Wiener a trouvé une attaque similaire mais sur des petits \(d\). Il démontra que si \(d < \frac{1}{3}n^{\frac{1}{4}}\), on peut retrouver \(d\), grâce à l'algorithme des fractions continues.
On part de l'équivalence suivante :
\(ed \equiv 1 \mod m\)
Par définition \(m = (p - 1) \times (q - 1)\), et \(ppcm(a, b) = \frac{| ab |}{pgcd(a, b)}\) (plus d'infos sur le ppcm), or \(p\) et \(q\) sont premiers entre eux, donc \(pgcd(p, q) = 1\), et on peut alors écrire :
\(ed \equiv 1 \mod ppcm(p - 1, q - 1)\)
Cela signifie qu'il existe un nombre entier \(K\), tel que :
\(ed = K \times ppcm(p - 1, q - 1) + 1\)
Soit \(G = pgcd(p - 1, q - 1)\), \(k = \frac{K}{pgcd(K, G)}\) et \(g = \frac{G}{pgcd(K, G)}\), on a la relation suivante :
\(ed = \frac{k}{g}(p - 1)(q - 1) + 1\)
Que l'on peut arranger en divisant le tout par \(dpq\) :
\(\frac{e}{pq} = \frac{k}{dg}(1 - \delta)\) avec \(\delta = \frac{p + q - 1 - \frac{g}{k}}{pq}\)
À partir de là, si on arrive à déterminer \(\frac{k}{dg}\) grâce à l'algorithme des fractions continues, on peut trouver \(k\) mais surtout \(dg\) qui nous permet de casser le système RSA.
Un article spécialement sur l'attaque de Wiener (et en français), montre comment utiliser l'algorithme des fractions continues : Attaque de clés RSA par la méthode de Wiener.
Créer un module de chiffrement à chaque génération de paires de clés peut être une opération lourde, et certaines personnes utilisaient un même \(n\) pour toutes les paires (avec bien entendu des \(e\) et \(d\) différents). À première vue, il n'y a pas de raison que ça ne fonctionne pas, cependant il a été démontré qu'une personne possédant une paire de clé de ce genre, peut factoriser assez facilement \(n\) avec son propre \(e\) et \(d\) et ainsi déduire les clés privées des autres personnes du système.

La démonstration vient de Twenty Years of Attacks on the RSA Cryptosystem de Dan Boneh, que vous pouvez retrouver en pdf sur Internet.
Et voici un exemple concret de l'utilisation de cette propriété pour factoriser \(n\) : How to factorize N given d.
En pratique, il est difficile de toujours faire une implémentation parfaite d'un système de chiffrement, et des études/audits révèlent régulièrement des failles dans certains systèmes de sécurité. Il est donc possible de se focaliser sur des attaques d'implémentations au lieu d'essayer de casser un système de chiffrement théorique.
L'idée consiste à étudier le temps nécessaire à l'ordinateur, stockant la clé privée, de déchiffrer (ou de signer) plusieurs messages. Cette attaque se base sur le fait que la plupart des implémentations utilisent un même algorithme (ou alors un algorithme connu) afin d'effectuer le déchiffrement, et on peut donc en déduire le nombre d'opérations effectuées et ainsi petit à petit récupérer des informations sur \(d\). Par exemple, il est courant d'utiliser l'exponentiation modulaire pour implémenter notre fonction de déchiffrement, comme nous avons vu précédemment, cependant une amélioration de cette dernière se base sur la représentation binaire de la clé (et donc de \(d\)), ce qui nous permet après plusieurs opérations de déchiffrement de faire des analyses statistiques sur les informations recueillies pour déterminer \(d\). Or, en général, une amélioration en temps est souvent cruciale en cryptographie, ceci est donc largement utilisé.
Tout d'abord, regardons l'amélioration de l'exponentiation modulaire :
Soit \(d\) notre exposant dans l'expression \(f'(x) = x^d \mod n\) avec \(x\) notre message chiffré. On peut écrire \(d\), sous forme de représentation binaire :
\(d = \displaystyle\sum_{i=0}^{b-1} a_i2^i\) avec \(a\) représentant un bit (soit 0 soit 1), et \(b\) le nombre de bit pour représenter \(d\).
On a donc \(x^d\) qu'on représente ainsi :
\(x^d = \displaystyle\prod_{i=0}^{b-1} (x^{2^i})^{a_i}\)
Cette représentation binaire permet de faire des opérations
extrêmement rapides dans la plupart des langages de programmation grâce
aux opérateurs bit à bit, en C par exemple on a les
opérateurs >> et << pour effectuer
des décalages (ou shift en anglais) sur des nombres binaires
(ceci offre notamment un gain énorme de temps sur des opérations comme
les puissances).
L'attaque par chronométrage consistera dans notre cas, à observer le temps que met l'ordinateur pour déchiffrer un certain message afin de trouver petit à petit chaque bit de \(d\). Tout d'abord, \(d\) par définition est forcément impair, on conclut donc que le bit 0 de \(d\) sera \(d_0 = 1\) (plus d'infos : bit de poids faible). Pour trouver les autres bits, on va émettre des hypothèses sur la valeur de \(a_i\), qui peut être soit 1, soit 0 (\(a_i\) n'est autre que le bit \(i\) de \(d\)). S'il est égal à 0, le résultat de \((b^{2^i})^{a_i}\) sera forcément 1, et l'opération sera alors bien plus rapide et différente en termes de temps qu'avec \(a_i = 1\), ce qui nous donne des informations sur des bits de \(d\). Il est possible d'utiliser ce principe afin de découvrir \(d\) en entier, simplement en demandant à l'ordinateur de déchiffrer des messages bien spécifiques.
Cette attaque ne s'applique pas uniquement à RSA, et peut être un aspect important de la sécurité d'une implémentation. Pour s'en protéger, on peut par exemple effectuer des délais dans le programme afin d'avoir un temps fixe pour chaque opération nécessaire, ou encore utiliser une technique d'aveuglement. Pour cette technique, avant de déchiffrer le message \(x\), l'ordinateur va prendre au hasard un nombre entier \(r\) et calculer \(x' = x \times r^e \mod n\), puis faire \(y' = x'^d \mod n\), et enfin \(y = \frac{y'}{r} \mod n\). Ces opérations sont en réalité un simple chiffrement/déchiffrement, mais en utilisant une variable intermédiaire \(r\) qui rend alors impossible l'attaque par chronométrage car \(r\) est choisi aléatoirement par l'ordinateur.
Sachez qu'il y a des attaques dans la même idée, mais se basant cette fois sur la consommation électrique de l'ordinateur qui peut varier en fonction des opérations effectuées lors du déchiffrement.
La dernière attaque traite un type d'exploitation de manière assez large car cela ne s'applique pas uniquement pour RSA. Mais de manière bien plus général, on trouve dans tous types de codes sources, et dans tous les domaines, des failles permettant de réaliser des attaques dessus. La cryptographie est loin d'être une exception et il y a énormément d'exemples d'attaques faites sur des systèmes après avoir trouvé des failles de sécurité importantes :
Heartbleed : en 2014, une découverte majeure dans la bibliothèque OpenSSL permettait de récupérer des informations secrètes à cause d'une erreur d'implémentation. La raison de cette attaque est que la librairie utilise une option appelée heartbeat qui permet de s'assurer que le client et le serveur sont toujours connectés, et elle fonctionne très simplement : le client envoie une requête au serveur avec une chaîne de caractères aléatoire, le serveur récupère la requête et renvoie la chaîne afin de montrer qu'il est toujours présent. Le problème était que la partie du code s'occupant de cette option ne vérifiait pas la taille indiquée dans la requête au sujet de la chaîne, c'est-à-dire que je pouvais envoyer cette chaîne au serveur "jIO91mq0x/" et dire qu'elle fait 42 caractères, le serveur va alors me renvoyer les 42 derniers caractères qu'il a en mémoire (dont la chaîne que je lui ai envoyée), ce qui peut rendre public des données sensibles comme des clés privées de chiffrement.
En début d'année 2016, une faille critique dans OpenSSH donnait accès aux clés privées SSH d'un utilisateur et donc détruisait toutes sécurités du système de chiffrement. Une option datant de 2010 (qui n'était même pas documentée) était activée par défaut sur un client OpenSSH et permettait de se reconnecter automatiquement à un serveur en cas de déconnexion soudaine. Cette option expérimentale présentait deux failles dont une permettait de récupérer les clés privées SSH d'un utilisateur : Exemple concret d'exploitation de cette faille
En 2015, une faille énorme dans le code des protocoles SSL/TLS d'Apple est découverte avec notamment ce fameux code qui a beaucoup circulé à ce propos :
if ((err = SSLHashSHA1.update(&hashCtx, &signedParams)) != 0)
goto fail;
goto fail;Où la ligne goto fail; est répétée deux fois ce qui
signifie qu'importe le résultat du test précédent, la fonction ira de
toute façon au label fail sautant alors tous les tests de
sécurité qui sont situés après. Ceci permettait à une personne
malveillante d'utiliser un certificat qui semblait être correct, mais
qui en réalité n'avait pas une bonne clé privée associée, afin d'avoir
une connexion sécurisée https qui paraissait authentique pour
l'utilisateur alors que ce n'était pas le cas.
Une recherche récente a été rendue public fin 2015 lors de la conférence 32 du Chaos Computer Club dans laquelle Alex Halderman et Nadia Heninger exposent une attaque consistant à forcer le serveur à utiliser d'anciens protocoles moins sécurisés que ceux de nos jours. La vidéo de la conférence (la partie concernant l'attaque commence à 18min13) : Logjam: Diffie-Hellman, discrete logs, the NSA, and you [32c3]
Même si peu après la découverte de ces failles, un patch a été rapidement proposé, certaines exploitations sont présentes et possibles depuis plusieurs années dans des systèmes et nécessitent bien plus de mises à jour de la part des utilisateurs. De nos jours, c'est une pratique régulière d'organiser des concours où le but est de découvrir le plus de failles et exploitations possibles dans une implémentation en échange d'argent pour la découverte. Cela permet de maintenir des systèmes importants en termes de sécurité, afin d'éviter toutes failles critiques dans l'implémentation.
Le système de chiffrement RSA est donc l'un des premiers algorithmes asymétriques garantissant une sécurité lors du chiffrement, mais surtout dans la transmission de la clé, en mettant en place des paires de clés publiques et privées. Sa sécurité est basée sur le fait qu'il est long et difficile de factoriser un nombre premier, et l'algorithme utilise plusieurs fonctions à sens unique afin de garantir la sécurité du message. Cependant s'il est mal utilisé ou que la sécurité est négligée (pour gagner du temps par exemple), quelques exploitations sont envisageables et même si aucunes n'est d'une importance majeure, elles ne sont pas à sous-estimer. De plus les implémentations d'un tel système sont parfois complexes à mettre en place, et ont bien plus de chance d'être vulnérable à des attaques que l'algorithme en lui-même. On découvre chaque année de nombreuses failles dans des systèmes utilisés mondialement, mais bien plus rarement des attaques cassant complètement un algorithme de chiffrement largement employé.
Aujourd'hui, les algorithmes de chiffrement asymétriques ne sont pas forcément le type d'algorithme le plus utilisé car chiffrer/déchiffrer un long message peut être très lent à cause des fonctions utilisées. En revanche, on utilisera plutôt un mélange entre les algorithmes symétriques et asymétriques afin de garder les avantages des deux types de chiffrement (opérations rapides de chiffrement/déchiffrement pour un algorithme symétrique, et transmission sécurisée de la clé pour un algorithme asymétrique). On appelle ce principe, la cryptographie hybride, et l'un des premiers systèmes de ce genre fut l'échange de clés Diffie-Hellman imaginé par Diffie et Hellman, qui sont à l'origine de l'utilisation d'algorithme de chiffrement asymétrique. Actuellement, la base d'un système de cryptographie hybride est souvent l'algorithme symétrique AES qui est très courant et fiable. Le gouvernement américain l'utilise comme standard et même jusqu'à des niveaux de classification top secrets, notamment grâce à sa rapidité et à sa robustesse (aucunes réelles attaques ne sont connues pour le moment sur ce système de chiffrement). L'algorithme RSA ne sera donc que rarement utilisé entièrement, mais plutôt partiellement grâce à la cryptographie hybride, utilisée par exemple dans OpenPGP ou encore GnuPG.
Cependant, une nouvelle ère dans le domaine de la cryptographie arrive : la cryptographie quantique. Cette dernière permettrait une transmission de la clé de manière totalement sécurisée et assurerait une protection garantie contre toutes techniques de cassage reposant sur des phénomènes physiques classiques (c'est-à-dire tous les phénomènes non quantiques). Un excellent talk à ce propos lors de la 32c3 :
Mais avec cette nouvelle technologie, se développe aussi les ordinateurs quantiques, basés sur les lois de la physique quantique et qui pourrait permettre théoriquement de casser n'importe quel système cryptographique moderne en très peu de temps. En effet, nos ordinateurs utilisent des phénomènes physiques dit classiques, possédant un seul état physique à la fois (0 ou 1 dans le cas des bits), mais les ordinateurs quantiques sont capables de prendre plusieurs états différents en même temps, grâce aux propriétés de la superposition ou encore de l'intrication. Ceci permettrait notamment de faire un nombre d'opérations considérables en une fraction de seconde car au lieu de les faire une par une, on pourrait théoriquement toutes les faire en même temps. Cette idée est loin d'être nouvelle, et en 1994, Peter Shor présenta l'algorithme de Shor qui permet de factoriser un nombre entier en un temps polynomial sur un ordinateur quantique. Pour le moment, nous sommes encore loin d'utiliser l'algorithme de Shor sur un ordinateur quantique pour casser des clés de chiffrement modernes, et même encore loin d'avoir un ordinateur quantique fiable et assez stable. Mais il faut savoir que cette technologie se développe rapidement, on entend beaucoup parler du fameux ordinateur quantique de D-Wave, et même si certains tests de rapidité sont assez controversés, ce domaine reste extrêmement intéressant et plein de potentiel pour de futures applications. Les ordinateurs quantiques nous permettraient de résoudre une quantité énorme de problèmes dont la solution nécessite trop de temps pour de simples ordinateurs non quantiques. Mais dans le domaine de la cryptographie, ce genre de technologie pose problème en termes de sécurité car nos systèmes de chiffrement actuels reposent sur des problèmes mathématiques que l'on ne sait pas résoudre rapidement avec des ordinateurs normaux (factorisation, logarithme discret, courbes elliptiques), et des chercheurs commencent donc déjà à chercher des algorithmes capables de résister à des attaques faites sur un ordinateur quantique pour se préparer au mieux à l'arrivée de ce genre d'ordinateur et à la cryptographie post-quantique.